怎么做二手网站代理做网站需要哪个系统
本教程教大家使用lua制作一个贪吃蛇,游戏引擎使用love2d,因为它开源轻巧而且跨平台。
1.开发环境搭建:
windows系统:
在windows系统下,首先我们进入官网www.love2d.org。
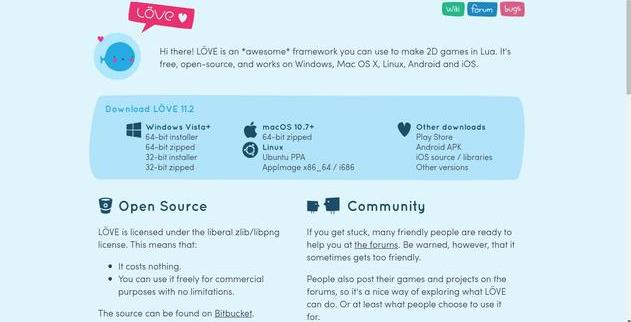
love2d官网

进入官网可以看到Download选项,在windows列表下,选择下载,如果你是32位 系统,那就选择32-bit,64位的选择64-bit。推荐下载installer,如果你下的是压缩包,那么你还需要自己配置环境变量,安装包则不需要,下载完成后只需要安装就可以了。
编辑器可以按照自己的习惯来,个人常用的编辑器是vim,当然你也可以使用vscode,sublime text,notepad等。
安装完成后双击love.exe,如果出现以下界面,代表环境搭建成功。

linux系统:
一般发行版都有love2d的包,可以从包下载安装,编辑器可以使用vim,个人的桌面环境为i3,方便开发。
在终端输入love出现以下non-game画面则安装成功。
2.测试
使用编辑器输入以下代码,保存为main.lua。
function love.draw() love.graphics.print("Hello World