禹城网站建设电话林业网站建设有哪些
使用过Excel的用户都知道,Excel可以方便的对数据进行分组,过滤,排序等操作,而在WPF中,默认提供的DataGrid只有很简单的功能,那么如何才能让我们开发的DataGrid,也像Excel一样具备丰富的客户端操作呢?今天就以一个简单的小例子,简述如何在WPF中实现DataGrid的过滤,分组,排序等功能。仅供学习分享使用,如有不足之处,还请指正。

涉及知识点
在本示例中,涉及知识点如下所示:
- CollectionView, CollectionView 类为实现 IEnumerable 接口的数据源提供分组和排序功能。
- CollectionViewSource,CollectionViewSource 类允许你从 XAML 设置 CollectionView 的属性。
注意:此两个类,是我们实现客户端过滤,分组,排序的关键。
普通绑定
1. 构建数据源
在WPF中,DataGrid的ItemSource属性用于绑定数据源,而数据源必须是实现IEnumerable接口的的列表类型,在本示例中,采用具有通知属性的列表类型ObservableCollection。当列表中元素数量发生变化时,可以实时的通知DataGrid进行刷新。
1.1 创建实体
在本示例中,为了测试,创建Student实体模型,如下所示:
public class Student
{public string No { get; set; }public string Name { get; set; }public int Age { get; set; }public bool Sex { get; set; }public string Class { get; set; }
}
1.2 初始化数据源列表
在本示例采用MVVM模式开发,在ViewModel中创建ObservableCollection类型的Students列表,如下所示:
using CommunityToolkit.Mvvm.ComponentModel;
using DemoDataGrid2.Models;
using System;
using System.Collections.Generic;
using System.Collections.ObjectModel;
using System.Linq;
using System.Text;
using System.Threading.Tasks;namespace DemoDataGrid2.ViewModels
{public class TestWindowViewModel:ObservableObject{private ObservableCollection<Student> students;public ObservableCollection<Student> Students{get { return students; }set { SetProperty(ref students, value); }}public TestWindowViewModel(){var parentName = new string[5] { "张", "王", "李", "赵", "刘" };this.Students = new ObservableCollection<Student>();for (int i = 0; i < 100; i++){Student student = new Student();student.No = i.ToString().PadLeft(3, '0');student.Name = parentName[(i % 4)] + i.ToString().PadLeft(2, 'A');student.Age = 20 + (i % 5);student.Sex = i % 2 == 0 ? true : false;student.Class = $"{(i % 3)}班";this.Students.Add(student);}}}
}
注意:构造函数中的方法,用于创建Students列表,包含100名学生,分别对应不同的编号,姓名,年龄,性别,班级等信息。
2. 页面绑定
在ViewModel中创建数据源后,可以在Xaml中进行绑定【语法:ItemsSource="{Binding Students}"】,如下所示:
<Window x:Class="DemoDataGrid2.TestWindow"xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"xmlns:d="http://schemas.microsoft.com/expression/blend/2008"xmlns:mc="http://schemas.openxmlformats.org/markup-compatibility/2006"xmlns:local="clr-namespace:DemoDataGrid2"mc:Ignorable="d"Title="DataGrid示例" Height="450" Width="800"><Grid><Grid.RowDefinitions><RowDefinition Height="Auto"></RowDefinition><RowDefinition></RowDefinition></Grid.RowDefinitions><DockPanel Grid.Row="0"></DockPanel><DataGrid Grid.Row="1" ItemsSource="{Binding Students}" AutoGenerateColumns="False" CanUserAddRows="False" CanUserDeleteRows="False" ><DataGrid.Columns><DataGridTextColumn Header="学号" Binding="{Binding No}" Width="*"></DataGridTextColumn><DataGridTextColumn Header="姓名" Binding="{Binding Name}" Width="*"></DataGridTextColumn><DataGridTextColumn Header="年龄" Binding="{Binding Age}" Width="*"></DataGridTextColumn><DataGridTemplateColumn Header="性别" Width="*"><DataGridTemplateColumn.CellTemplate><DataTemplate><TextBlock x:Name="sex"><TextBlock.Style><Style TargetType="TextBlock"><Style.Triggers><DataTrigger Binding="{Binding Sex}" Value="True"><Setter Property="Text" Value="男"></Setter></DataTrigger><DataTrigger Binding="{Binding Sex}" Value="False"><Setter Property="Text" Value="女"></Setter></DataTrigger></Style.Triggers></Style></TextBlock.Style></TextBlock></DataTemplate></DataGridTemplateColumn.CellTemplate></DataGridTemplateColumn><DataGridTextColumn Header="班级" Binding="{Binding Class}" Width="*"></DataGridTextColumn></DataGrid.Columns></DataGrid></Grid>
</Window>
以下两点需要注意:
- 在本示例中,性别为bool类型,要转换成汉字,用到了DataTrigger。
- DataGrid的列可以自动生成,也可以手动创建,可以通过AutoGenerateColumns="False"来设置。
3. 普通绑定示例
普通绑定示例截图,如下所示:

DataGrid过滤
在DataGrid中,实现客户端过滤,且不需要重新初始化数据源,则需要用到CollectionViewSource。
1. 定义资源及绑定
将CollectionViewSource定义成一种资源,并将资源的Source属性绑定到数据源,再将DataGrid中的ItemSource绑定到此资源,然后就可以在过滤时对资源进行过滤。
定义资源如下所示:
<Window.Resources><CollectionViewSource x:Key="cvStudents" Source="{Binding Students}"></CollectionViewSource>
</Window.Resources>
DataGrid绑定资源【语法:ItemsSource="{Binding Source={StaticResource cvStudents}}"】,如下所示:
<DataGrid x:Name="dgStudents" Grid.Row="1" ItemsSource="{Binding Source={StaticResource cvStudents}}" AutoGenerateColumns="False" CanUserAddRows="False" CanUserDeleteRows="False" ><DataGrid.Columns><DataGridTextColumn Header="学号" Binding="{Binding No}" Width="*"></DataGridTextColumn><DataGridTextColumn Header="姓名" Binding="{Binding Name}" Width="*"></DataGridTextColumn><DataGridTextColumn Header="年龄" Binding="{Binding Age}" Width="*"></DataGridTextColumn><DataGridTemplateColumn Header="性别" Width="*"><DataGridTemplateColumn.CellTemplate><DataTemplate><TextBlock x:Name="sex"><TextBlock.Style><Style TargetType="TextBlock"><Style.Triggers><DataTrigger Binding="{Binding Sex}" Value="True"><Setter Property="Text" Value="男"></Setter></DataTrigger><DataTrigger Binding="{Binding Sex}" Value="False"><Setter Property="Text" Value="女"></Setter></DataTrigger></Style.Triggers></Style></TextBlock.Style></TextBlock></DataTemplate></DataGridTemplateColumn.CellTemplate></DataGridTemplateColumn><DataGridTextColumn Header="班级" Binding="{Binding Class}" Width="*"></DataGridTextColumn></DataGrid.Columns>
</DataGrid>
2. 过滤条件
在本示例中,以性别为过滤条件,当点击过滤条件时,触发过滤命令,如下所示:
<DockPanel Grid.Row="0" Margin="5"><TextBlock Text="筛选条件:"></TextBlock><TextBlock Text="性别:"></TextBlock><CheckBox Content="男" IsChecked="{Binding FilterM.IsMaleChecked}" Command="{Binding FiterSexCheckedCommand}"></CheckBox><CheckBox Content="女" IsChecked="{Binding FilterM.IsFemaleChecked}" Command="{Binding FiterSexCheckedCommand}"></CheckBox>
</DockPanel>
当用户点击时,触发Command绑定的命令,如下所示:
private ICommand fiterSexCheckedCommand;public ICommand FiterSexCheckedCommand
{get{if (fiterSexCheckedCommand == null){fiterSexCheckedCommand = new RelayCommand<object>(FilterSexChecked);}return fiterSexCheckedCommand;}
}private void FilterSexChecked(object obj)
{if (this.dataGrid != null){ICollectionView cvs = CollectionViewSource.GetDefaultView(this.dataGrid.ItemsSource);if (cvs != null && cvs.CanFilter){cvs.Filter = (object obj) =>{bool flag = true;bool flag1 = true;bool flag2 = true;var student = obj as Student;if (!FilterM.IsMaleChecked){flag1 = student.Sex != true;}if (!FilterM.IsFemaleChecked){flag2 = student.Sex != false;}flag = flag1 && flag2;return flag;};}}
}
注意:通过CollectionViewSource.GetDefaultView(this.dataGrid.ItemsSource)方法获取具有过滤功能的CollectionView类对象,然后再对Filter进行委托即可。
其中FilterM是在ViewModel中声明的FilterConditionM类型的属性。
private FilterConditionM filterM;public FilterConditionM FilterM
{get { return filterM; }set { SetProperty(ref filterM, value); }
}
FilterConditionM是封装的过滤条件模型类, 如下所示:
namespace DemoDataGrid2.Models
{public class FilterConditionM:ObservableObject{private bool isMaleChecked;public bool IsMaleChecked{get { return isMaleChecked; }set { SetProperty(ref isMaleChecked , value); }}private bool isFemaleChecked;public bool IsFemaleChecked{get { return isFemaleChecked; }set { SetProperty(ref isFemaleChecked, value); }}}
}
3. 过滤功能示例
具备过滤功能的示例截图,如下所示:

DataGrid分组
在WPF中,实现DataGrid的分组,也是通过CollectionViewSource来实现。
1. 设置分组列
有两种方式可以设置分组
1.1 XAML中设置
在XAML中,通过设置CollectionViewSource的GroupDescriptions属性,来设置具体分组的列属性,如下所示:
<CollectionViewSource x:Key="cvStudents" Source="{Binding Students}"><CollectionViewSource.GroupDescriptions><PropertyGroupDescription PropertyName="Class"/><PropertyGroupDescription PropertyName="Sex"/></CollectionViewSource.GroupDescriptions>
</CollectionViewSource>
1.2 后台代码设置
在ViewModel中设置CollectionView的GroupDescriptions属性,如下所示:
ICollectionView cvTasks = CollectionViewSource.GetDefaultView(this.dataGrid.ItemsSource);
if (cvTasks != null && cvTasks.CanGroup == true)
{cvTasks.GroupDescriptions.Clear();cvTasks.GroupDescriptions.Add(new PropertyGroupDescription("Class"));cvTasks.GroupDescriptions.Add(new PropertyGroupDescription("Sex"));
}
2. 设置分组样式
在WPF中,通过设置DataGrid的GroupStyle属性来改变分组样式,如下所示:
<DataGrid x:Name="dgStudents" Grid.Row="1" ItemsSource="{Binding Source={StaticResource cvStudents}}" AutoGenerateColumns="False" CanUserAddRows="False" CanUserDeleteRows="False" ><DataGrid.GroupStyle><!-- 第一层分组 --><GroupStyle><GroupStyle.ContainerStyle><Style TargetType="{x:Type GroupItem}"><Setter Property="Margin" Value="0,0,0,5"/><Setter Property="Template"><Setter.Value><ControlTemplate TargetType="{x:Type GroupItem}"><Expander IsExpanded="True" Background="LightGray" BorderBrush="#FF002255" Foreground="DarkBlue" BorderThickness="1"><Expander.Header><DockPanel><TextBlock FontWeight="Bold" Text="{Binding Path=Name}" Margin="5"/><TextBlock FontWeight="Bold" Text=" 班 , " VerticalAlignment="Center"></TextBlock><TextBlock FontWeight="Bold" Text="{Binding Path=ItemCount}" VerticalAlignment="Center"/><TextBlock FontWeight="Bold" Text=" 名学生" VerticalAlignment="Center"></TextBlock></DockPanel></Expander.Header><Expander.Content><ItemsPresenter /></Expander.Content></Expander></ControlTemplate></Setter.Value></Setter></Style></GroupStyle.ContainerStyle></GroupStyle><!-- 第二层及之后的分组 --><GroupStyle><GroupStyle.HeaderTemplate><DataTemplate><DockPanel Background="LightGoldenrodYellow"><TextBlock Foreground="Blue" Margin="30,0,0,0" Width="30"><TextBlock.Style><Style TargetType="TextBlock"><Style.Triggers><DataTrigger Binding="{Binding Path=Name}" Value="True"><Setter Property="Text" Value="男"></Setter></DataTrigger><DataTrigger Binding="{Binding Path=Name}" Value="False"><Setter Property="Text" Value="女"></Setter></DataTrigger></Style.Triggers></Style></TextBlock.Style></TextBlock><TextBlock Text="{Binding Path=ItemCount}" Foreground="Blue"/></DockPanel></DataTemplate></GroupStyle.HeaderTemplate></GroupStyle></DataGrid.GroupStyle><DataGrid.Columns><DataGridTextColumn Header="学号" Binding="{Binding No}" Width="*"></DataGridTextColumn><DataGridTextColumn Header="姓名" Binding="{Binding Name}" Width="*"></DataGridTextColumn><DataGridTextColumn Header="年龄" Binding="{Binding Age}" Width="*"></DataGridTextColumn><DataGridTemplateColumn Header="性别" Width="*"><DataGridTemplateColumn.CellTemplate><DataTemplate><TextBlock x:Name="sex"><TextBlock.Style><Style TargetType="TextBlock"><Style.Triggers><DataTrigger Binding="{Binding Sex}" Value="True"><Setter Property="Text" Value="男"></Setter></DataTrigger><DataTrigger Binding="{Binding Sex}" Value="False"><Setter Property="Text" Value="女"></Setter></DataTrigger></Style.Triggers></Style></TextBlock.Style></TextBlock></DataTemplate></DataGridTemplateColumn.CellTemplate></DataGridTemplateColumn><DataGridTextColumn Header="班级" Binding="{Binding Class}" Width="*"></DataGridTextColumn></DataGrid.Columns>
</DataGrid>
DataGrid排序
在WPF中,实现DataGrid的排序,也是通过CollectionViewSource来实现。
1. 设置排序列
有两种方式可以设置DataGrid排序列,如下所示:
1.1 XAML中设置
通过设置CollectionViewSource的SortDescriptions属性,设置排序列和排序方向。如下所示:
<CollectionViewSource x:Key="cvStudents" Source="{Binding Students}"><CollectionViewSource.SortDescriptions><scm:SortDescription PropertyName="No" Direction="Ascending"/><scm:SortDescription PropertyName="Age" Direction="Descending"/></CollectionViewSource.SortDescriptions>
</CollectionViewSource>
其中scm是新定义的命名空间【xmlns:scm="clr-namespace:System.ComponentModel;assembly=WindowsBase"】
1.2 后台代码设置
在ViewModel中通过后台代码设置,同样也需要引入对应的命名空间,如下所示:
ICollectionView cvTasks = CollectionViewSource.GetDefaultView(this.dataGrid.ItemsSource);
if (cvTasks != null && cvTasks.CanSort == true)
{cvTasks.SortDescriptions.Clear();cvTasks.SortDescriptions.Add(new SortDescription("No", ListSortDirection.Ascending));cvTasks.SortDescriptions.Add(new SortDescription("Age", ListSortDirection.Ascending));
}
DataGrid整体示例
具备过滤,分组,排序的示例截图,如下所示:
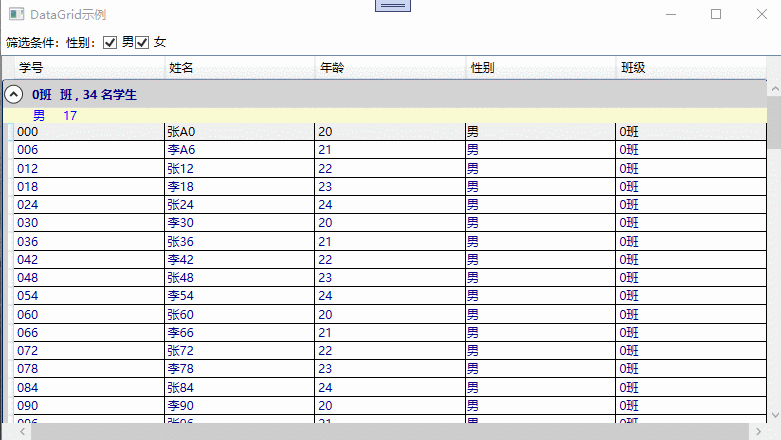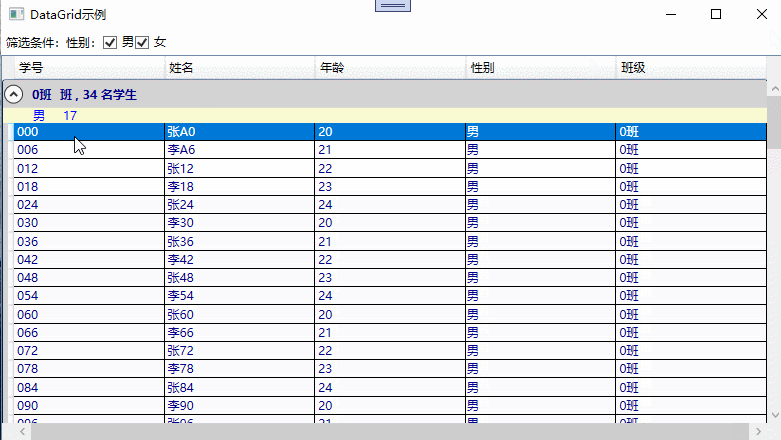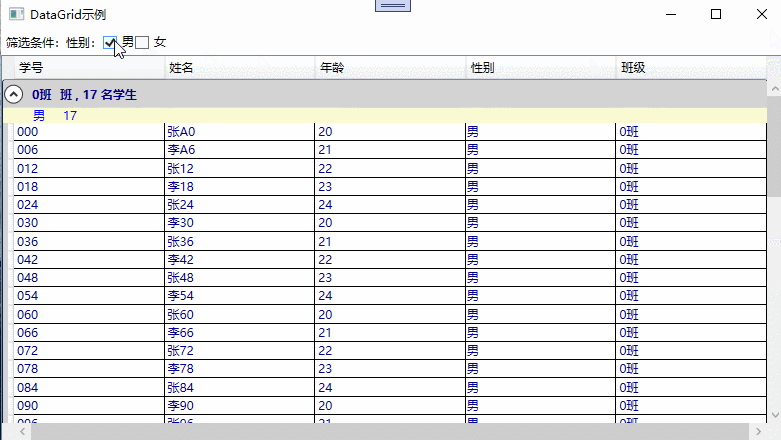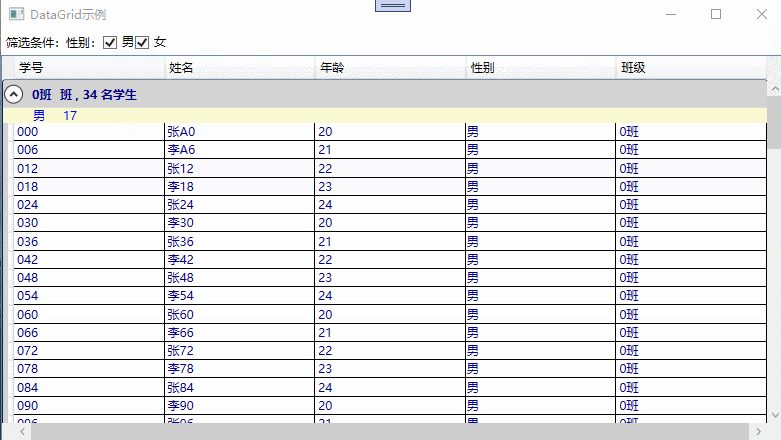
参考文献
1. 官方文档:https://learn.microsoft.com/zh-cn/dotnet/desktop/wpf/controls/how-to-group-sort-and-filter-data-in-the-datagrid-control?view=netframeworkdesktop-4.8
以上就是【浅谈WPF之DataGrid过滤,分组,排序】的全部内容,希望能够一起学习,共同进步。
