网站在哪里搜索wordpress后台主题

🏡作者主页:点击!
🤖编程探索专栏:点击!
⏰️创作时间:2024年11月16日13点39分

神秘男子影,
秘而不宣藏。
泣意深不见,
男子自持重,
子夜独自沉。
论文链接
点击开启你的论文编程之旅![]() https://www.aspiringcode.com/content?id=17087924951368&uid=a759ff2cd7ac43f1ab9d3ffda5684bd2
https://www.aspiringcode.com/content?id=17087924951368&uid=a759ff2cd7ac43f1ab9d3ffda5684bd2
文献参考
下面我将使用Pytorch框架来对《Sentiment analysis method based on sentiment lexicon and Transformer》一文中的Transformer情感分类器进行实现,在这里,我使用现有的2022年英文股评数据集作为初始数据,为其创建情感词典,实现句子转向量并完成Transformer模型的训练过程。
概述
由于Transformer模型的强大表征学习能力,可以在大规模文本数据上进行预训练,并且具有适用性广泛的特点,因此Transformer模型已经被广泛应用于自然语言处理领域,它能够各种任务上取得了优异的表现,包括情感分析。本篇使用股票市场上的股民评论数据作为训练数据,股票市场受到投资者情绪和情感的影响很大,通过对股票评论进行情感分析,可以帮助分析师和投资者更好地了解市场参与者的情绪状态,从而预测市场走势;同时针对股评的情感分析还能帮助公司和投资者监控舆论动向,帮助投资者更好地理解市场参与者的情绪和看法,为投资决策提供参考。
演示效果
众所周知,Transformer模型主要由encoder和decoder两部分组成,它们各自承担着不同的功能和作用。
Encoder:
用途:Encoder部分负责将输入序列(比如文本)转换为一系列隐藏表示,捕获输入序列中的信息和特征。
区别:每个输入词语都经过embedding层后进入encoder,然后通过多层的自注意力机制和前馈神经网络进行特征提取和编码,最终得到输入序列的表示。
Decoder:
用途:Decoder部分负责使用encoder生成的表示来预测输出序列(比如机器翻译中的翻译结果)。
区别:与encoder不同,decoder在处理每个位置的时候会利用encoder输出的信息,并且具有额外的掩码机制来确保在预测时不会使用未来的信息。、
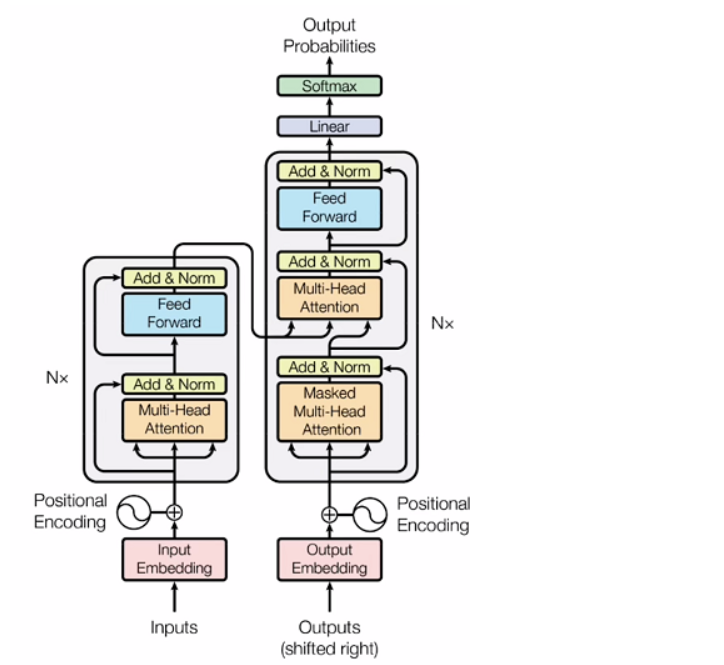
进行情感分析的Transformer模型通常是在完整的Transformer模型基础上进行微调或修改的,主要是为了适应情感分析任务的特点和需求。在情感分析任务中,通常会对输入文本进行一定的处理,如添加特殊标记或截断,以适应模型输入的要求。此外,可能会在输入文本前后添加特殊标记来指示情感分析任务。而模型的输出是对结果的三分类(或者二分类)结果。
要将文本数据变成能够放入模型中的训练数据集,我们需要基于目前已有的股评文本,构建本地可用的词典,并把文本序列转换成一系列长度一致的词向量,如下图:

对应到代码中则可以分成下面几个步骤:
1,将句中字母小写,情感标签映射到【0,1,2】列表中
2,去除特殊字符
3,去除停用词,这需要导入包含英文停用词的数据包
4,将单词进行词性还原
5,将单词与数字一一对应,实现句子转向量
df.text_sentiment.unique()
df.drop_duplicates(inplace=True) ### 删除重复值
pd.factorize(df.text_sentiment) ### 0:Neutral 1:Negative 2:Positive### 将情感标签映射为【0,1,2】label = pd.factorize(df.text_sentiment)[0]### 全部变为小写字母,不保留除’之外标点符号,去除特殊字符
pat = re.compile('[A-Za-z\']+')def pre_text(text):text = pat.findall(text) ### 返回列表text = [w.lower() for w in text]return text
x = df.text.apply(pre_text) ### 去除停用词
def stop_words_filter(text): text= [w for w in text if w not in stopwords.words('english') ]return text
x = x.apply(stop_words_filter) ### 词形还原,利用wordnet
wnl = WordNetLemmatizer()
def return_words(text):text = [wnl.lemmatize(w) for w in text]return text
for text in x:text = [return_words(text)] ### 创建词表,将每个词映射到词表上
word_set = set()
for t in x:for word in t:word_set.add(word)
max_word = len(word_set)+2 ### 词表总长+2, 留下unknow和padding,后面万一进入与这些词不同的词就映射到unk上,序列padding的部分就映射到pad上word_list = list(word_set)
word_index = dict((w,word_list.index(w)+1) for w in word_list)
x = x.apply(lambda t:[word_index.get(w) for w in t]) ###统一向量长度,将每句话padding为长度相同的列表
maxlen = max(len(t) for t in x)
pad_x = [t+ (maxlen-len(t))*[0] for t in x]
pad_x = np.array(pad_x)
# 将 ndarray 转换为 DataFrame
df_pad_x = pd.DataFrame(pad_x)
df_label = pd.DataFrame(label, columns=['label'])
df_pad_x_reset = df_pad_x.reset_index(drop=True)
df_label_reset = df_label.reset_index(drop=True)
df_output = pd.concat([df_pad_x_reset, df_label_reset],axis=1) #保存数据
df_output.to_csv('df_output.csv', index=False)核心逻辑
得到向量化的训练数据后,我们对应上面的Transformer结构图中左半部分的encoder编码器,我们构建了一个主体由encoder与softmax分类器组成的Transformer情感分类器
import torch
import torch.nn as nn#参数配置
embed_dim =37411 # 字 Embedding 的维度
d_model=256
d_ff = 1024 # 前向传播隐藏层维度
d_k = d_v = 64 # K(=Q), V的维度
n_layers = 3 # 有多少个encoder
n_heads = 4 # Multi-Head Attention设置为8
seq_len=54
batch_size=64
src_vocab_size=37411
tgt_vocab_size=3
dropout=0.1#te 和 pe 都是形状为 (batch_size, seq_len, embed_dim) 的张量
class PositionalEncoding(nn.Module): #nn.Module是一个用于构建神经网络模型的基类def __init__(self):super(PositionalEncoding, self).__init__()self.d_model=d_modelself.seq_len=seq_lenself.dropout = nn.Dropout(p=dropout)pos_table = np.array([[pos / np.power(10000, 2 * i / d_model) for i in range(d_model)]if pos != 0 else np.zeros(d_model) for pos in range(seq_len)])pos_table[1:, 0::2] = np.sin(pos_table[1:, 0::2]) # 字嵌入维度为偶数时pos_table[1:, 1::2] = np.cos(pos_table[1:, 1::2]) # 字嵌入维度为奇数时self.pos_table = torch.LongTensor(pos_table).to(device)def forward(self, enc_inputs): # enc_inputs: [batch_size, seq_len, d_model] 32*54*100#enc_inputs = torch.from_numpy(enc_inputs).to(torch.int64) # 转换为LongTensor类型 enc_inputs += self.pos_table[:enc_inputs.size(1), :] #self.pos_table[:54, :]return self.dropout(enc_inputs.to(device)) #[batch_size, seq_len, d_model] 32*54*100def get_attn_pad_mask(seq_q, seq_k): # seq_q: [batch_size, seq_len] ,seq_k: [batch_size, seq_len] 32*54batch_size, len_q = seq_q.size()batch_size, len_k = seq_k.size()pad_attn_mask = seq_k.data.eq(0).unsqueeze(1) # 判断 输入那些含有P(=0),用1标记 ,[batch_size, 1, len_k]return pad_attn_mask.expand(batch_size, len_q, len_k) # 扩展成多维度def get_attn_subsequence_mask(seq): # seq: [batch_size, tgt_len] 32*3attn_shape = [seq.size(0), seq.size(1), seq.size(1)]subsequence_mask = np.triu(np.ones(attn_shape), k=1) # 生成上三角矩阵,[batch_size, tgt_len, tgt_len]subsequence_mask = torch.from_numpy(subsequence_mask).byte() # [batch_size, tgt_len, tgt_len]return subsequence_mask #32*3*3class ScaledDotProductAttention(nn.Module):#给定一个查询向量Q、一个键向量K、一个值向量V和一个注意力掩码attn_mask,#该模块会计算出每个查询向量对应的上下文向量context和注意力矩阵attn。def __init__(self):super(ScaledDotProductAttention, self).__init__()def forward(self, Q, K, V, attn_mask): # Q: [batch_size, n_heads, len_q, d_k] 32*3*64 # attn_mask: [batch_size, n_heads, seq_len, seq_len]scores = torch.matmul(Q, K.transpose(-1, -2)) / np.sqrt(d_k) # scores : [batch_size, n_heads, len_q, len_k]scores.masked_fill_(attn_mask, -1e9) # 如果时停用词P就等于 0attn = nn.Softmax(dim=-1)(scores)context = torch.matmul(attn, V) # [batch_size, n_heads, len_q, d_v]return context, attnclass MultiHeadAttention(nn.Module): #输入QKV和attn_mask四个矩阵def __init__(self):super(MultiHeadAttention, self).__init__()
# assert n_heads == d_model//d_k
# d_k = d_model//n_headsself.W_Q = nn.Linear(d_model, d_k * n_heads, bias=False)self.W_K = nn.Linear(d_model, d_k * n_heads, bias=False)self.W_V = nn.Linear(d_model, d_v * n_heads, bias=False)self.fc = nn.Linear(n_heads * d_v, d_model, bias=False)def forward(self, input_Q, input_K, input_V, attn_mask): # input_Q: [batch_size, len_q, d_model]# input_K: [batch_size, len_k, d_model]# input_V: [batch_size, len_v(=len_k), d_model]# attn_mask: [batch_size, seq_len, seq_len]residual, batch_size = input_Q, input_Q.size(0)Q = self.W_Q(input_Q).view(batch_size, -1, n_heads, d_k).transpose(1, 2) # Q: [batch_size, n_heads, len_q, d_k]K = self.W_K(input_K).view(batch_size, -1, n_heads, d_k).transpose(1, 2) # K: [batch_size, n_heads, len_k, d_k]V = self.W_V(input_V).view(batch_size, -1, n_heads, d_v).transpose(1, 2) # V: [batch_size, n_heads, len_v(=len_k), d_v]attn_mask = attn_mask.unsqueeze(1).repeat(1, n_heads, 1, 1) # attn_mask : [batch_size, n_heads, seq_len, seq_len]context, attn = ScaledDotProductAttention()(Q, K, V, attn_mask) # context: [batch_size, n_heads, len_q, d_v]# attn: [batch_size, n_heads, len_q, len_k]context = context.transpose(1, 2).reshape(batch_size, -1,n_heads * d_v) # context: [batch_size, len_q, n_heads * d_v]output = self.fc(context) # [batch_size, len_q, d_model]#return nn.LayerNorm(d_model).cuda()(output + residual), attnreturn nn.LayerNorm(d_model).to(device)(output + residual), attnclass PoswiseFeedForwardNet(nn.Module):def __init__(self):super(PoswiseFeedForwardNet, self).__init__()self.fc = nn.Sequential(nn.Linear(d_model, d_ff, bias=False),nn.ReLU(),nn.Linear(d_ff, d_model, bias=False))def forward(self, inputs): # inputs: [batch_size, seq_len, d_model] 32*54*100residual = inputsoutput = self.fc(inputs)return nn.LayerNorm(d_model).to(device)(output + residual) # [batch_size, seq_len, d_model] 32*54*100class EncoderLayer(nn.Module):def __init__(self):super(EncoderLayer, self).__init__()self.enc_self_attn = MultiHeadAttention() # 多头注意力机制self.pos_ffn = PoswiseFeedForwardNet() # 前馈神经网络def forward(self, enc_inputs, enc_self_attn_mask): # enc_inputs: [batch_size, src_len, d_model]# 输入3个enc_inputs分别与W_q、W_k、W_v相乘得到Q、K、V # enc_self_attn_mask: [batch_size, src_len, src_len]enc_outputs, attn = self.enc_self_attn(enc_inputs, enc_inputs, enc_inputs,# enc_outputs: [batch_size, src_len, d_model],enc_self_attn_mask) # attn: [batch_size, n_heads, src_len, src_len]enc_outputs = self.pos_ffn(enc_outputs) # enc_outputs: [batch_size, src_len, d_model]return enc_outputs, attnclass Encoder(nn.Module):def __init__(self):super(Encoder, self).__init__()self.src_emb = nn.Embedding(src_vocab_size, d_model) # 把字转换字向量self.pos_emb = PositionalEncoding() # 加入位置信息self.layers = nn.ModuleList([EncoderLayer() for _ in range(n_layers)])def forward(self, enc_inputs): # enc_inputs: [batch_size, src_len] 32*54enc_outputs = self.src_emb(enc_inputs) # enc_outputs: [batch_size, src_len, d_model]enc_outputs = self.pos_emb(enc_outputs) # enc_outputs: [batch_size, src_len, d_model]enc_self_attn_mask = get_attn_pad_mask(enc_inputs, enc_inputs) # enc_self_attn_mask: [batch_size, src_len, src_len]enc_self_attns = []for layer in self.layers:enc_outputs, enc_self_attn = layer(enc_outputs, enc_self_attn_mask) # enc_outputs : [batch_size, src_len, d_model], # enc_self_attn : [batch_size, n_heads, src_len, src_len]enc_self_attns.append(enc_self_attn)return enc_outputs, enc_self_attnsclass Transformer(nn.Module):def __init__(self):super(Transformer, self).__init__()self.src_vocab_size = src_vocab_sizeself.tgt_vocab_size = tgt_vocab_sizeself.Encoder = Encoder().to(device)self.projection = nn.Linear(d_model, tgt_vocab_size).to(device)def forward(self, enc_inputs):enc_outputs, enc_self_attns = self.Encoder(enc_inputs) # enc_outputs: [batch_size, seq_len, d_model]enc_outputs = torch.mean(enc_outputs,dim=1)output = self.projection(enc_outputs)return output搭建好的Transformer情感分类器即主要由以上数个函数组成,随后我们利用处理好的数据使模型完成预训练,需要注意的是,各部分的输入输出数据维度要能够衔接得上,模型的参数设置也有一定的讲究,这里我设置每次训练取的数据量batch_size为64,也可以取更大的值加快模型训练过程但训练效果不一定更优
import torch
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
#读入数据,共30000+条数据
data=pd.read_csv('df_output.csv')
y=data['label']
y=np.array(y)
del data['label']
X=np.array(data)
x_train,x_test,y_train,y_test=train_test_split(X, y, test_size=0.2, random_state=42)
# 将 x_train 和 y_train 转换为张量类型
x_train,x_test,y_train,y_test=torch.tensor(x_train),torch.tensor(x_test),torch.tensor(y_train),torch.tensor(y_test)
# 将张量类型的数据打包成 TensorDataset
dataset1 = torch.utils.data.TensorDataset(x_train, y_train)
dataset2 = torch.utils.data.TensorDataset(x_test, y_test)
train_loader = Data.DataLoader(dataset1, batch_size, shuffle=True)
test_loader = Data.DataLoader(dataset2, batch_size, shuffle=True)#进行25轮次模型训练与参数寻优import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
import torch.utils.data as Data# 定义优化器
src_idx2word = {0: "Natural",1: "Negative",2: "Positive"
}
device = torch.device("cpu")
model = Transformer().to(device)
train_accuracy_values=[]
test_accuracy_values=[]criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.05,weight_decay=0.01)n=25
#进行n轮的模型运算
for epoch in range(n):correct_predictions1 = 0total_predictions1 = 0correct_predictions2 = 0total_predictions2 = 0combined_loader = Data.DataLoader(dataset1, batch_size, shuffle=True)for a,(inputs,labels) in enumerate(combined_loader):optimizer.zero_grad()outputs = model.forward(torch.tensor(inputs))outputs = torch.squeeze(outputs) # 去除维度为1的维度# 将模型输出经过Sigmoid激活函数处理loss = criterion(outputs, labels.long()) # 计算损失output=nn.functional.softmax(outputs,dim=1)loss.backward()optimizer.step()# Calculate accuracy_, predicted = torch.max(outputs, 1)#print(predicted)total_predictions1 += labels.view(-1).size(0)correct_predictions1 += (predicted == labels.view(-1)).sum().item()#测试过程new_loader = Data.DataLoader(dataset2, batch_size, shuffle=True)with torch.no_grad():for a,(inputs,labels) in enumerate(new_loader):outputs = model.forward(torch.tensor(inputs))outputs = torch.squeeze(outputs) # 去除维度为1的维度# 将模型输出经过Sigmoid激活函数处理loss = criterion(outputs, labels.long()) # 计算损失output=nn.functional.softmax(outputs,dim=1)# Calculate accuracy_, predicted = torch.max(outputs, 1)#print(predicted)total_predictions2 += labels.view(-1).size(0)correct_predictions2 += (predicted == labels.view(-1)).sum().item()# Calculate and append the average loss and accuracy for the epochtrain_accuracy = (correct_predictions1 / total_predictions1) * 100train_accuracy_values.append(train_accuracy)test_accuracy = (correct_predictions2 / total_predictions2) * 100test_accuracy_values.append(test_accuracy)print('Epoch:', '%04d' % (epoch + 1), 'train_accuracy =', '{:.2f}%'.format(train_accuracy))print('Epoch:', '%04d' % (epoch + 1), 'test_accuracy =', '{:.2f}%'.format(test_accuracy))
torch.save(model,'model.pth')由于数据量与参数量庞大且本人使用的是CPU内核,因此上述训练过程耗费时长达到4个小时,将模型训练结果绘制成曲线则如下图
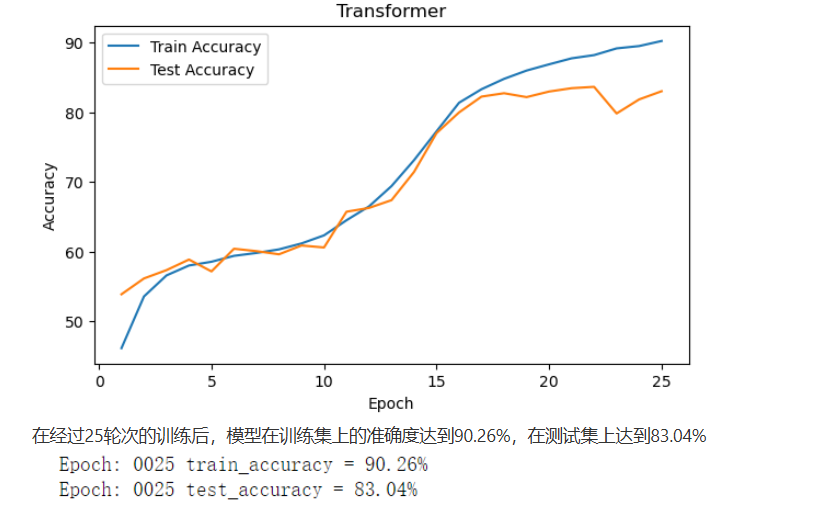
使用方式
将上述训练好的模型与“文本to向量”转换器之间进行衔接之后,最终得到期望的Transformer情感分类器,模型的输入格式为英文文本内容,输出为Positive,Negative或者Normal这三类情感标签之一。
例如:输入:“It’s incredible. I didn’t think it could flip or even go up.”
输出:“Positive”
部署方式
pythorch Python3.11
成功的路上没有捷径,只有不断的努力与坚持。如果你和我一样,坚信努力会带来回报,请关注我,点个赞,一起迎接更加美好的明天!你的支持是我继续前行的动力!"
"每一次创作都是一次学习的过程,文章中若有不足之处,还请大家多多包容。你的关注和点赞是对我最大的支持,也欢迎大家提出宝贵的意见和建议,让我不断进步。"
神秘泣男子

