网站机房建设流程佛山网站优化如何
- HTTPS 协议原理
- 加密
- 为什么要加密
- 常见的加密方式
- 对称加密
- 非对称加密
- 数据摘要&&数据指纹
- HTTPS 的工作过程探究
- 方案1-只使用对称加密
- 方案2-只使用非对称加密
- 方案3-双方都使用非对称加密
- 方案4-非对称加密+对称加密
- 中间人攻击-针对上面的场景
- CA认证
- 理解数据签名
- 方案5-非对称加密+对称加密+证书认证
- 完整流程
HTTPS 协议原理
HTTPS 是什么?
HTTPS 也是⼀个应用层协议。是在 HTTP 协议的基础上引入了⼀个加密层。
HTTP 协议内容都是按照文本的方式明文传输的。这就导致在传输过程中出现⼀些被篡改的情况
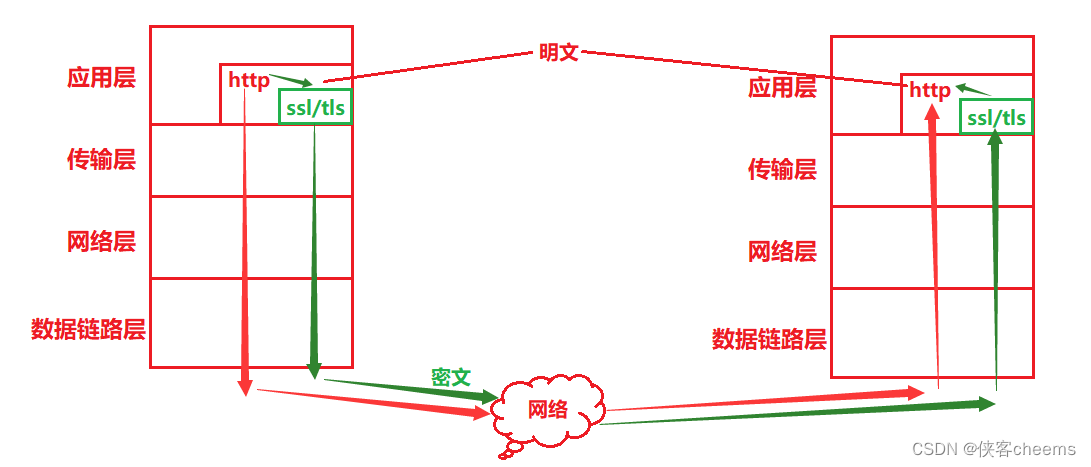
加密
加密就是把 明文 (要传输的信息)进行⼀系列变换,生成 密文 。
解密就是把 密文 再进行⼀系列变换,还原成 明文 。
在这个加密和解密的过程中,往往需要⼀个或者多个中间的数据,辅助进行这个过程,这样的数据称为 密钥。
举例:只有发出方和接收方最后能得到原始数据,中间流通的都是密文
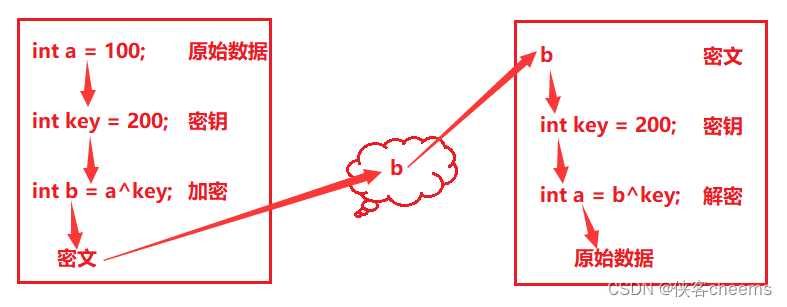
为什么要加密
臭名昭著的 “运营商劫持”
下载⼀个 天天动听,未被劫持的效果,点击下载按钮,就会弹出天天动听的下载链接。
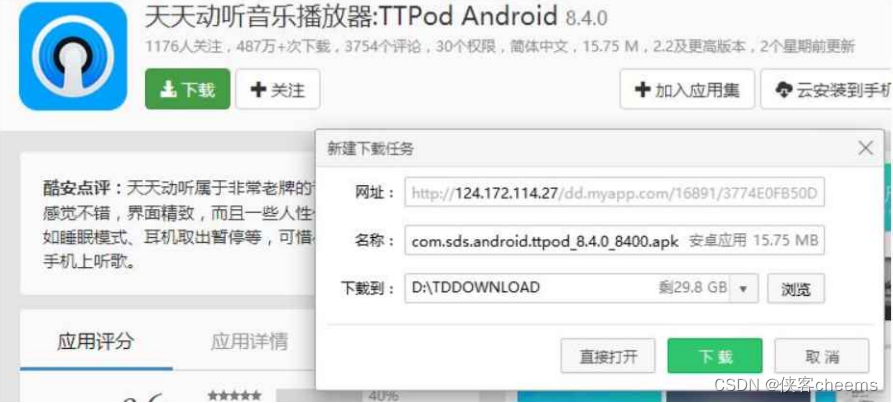
已被劫持的效果, 点击下载按钮, 就会弹出 QQ 浏览器的下载链接
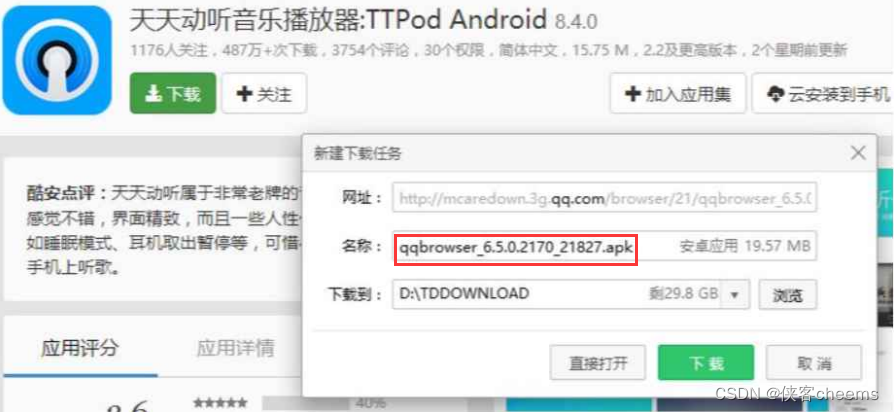
由于我们通过网络传输的任何的数据包都会经过运营商的网络设备(路由器、交换机等),那么运营商的网络设备就可以解析出你传输的数据内容,并进行篡改。
点击"下载按钮",其实就是在给服务器发送了一个HTTP请求,获取到的HTTP响应其实就包含了该APP的下载链接。运营商劫持之后,就发现这个请求是要下载天天动听,那么就自动的把交给用户的响应给篡改成"QQ浏览器"的下载地址了。
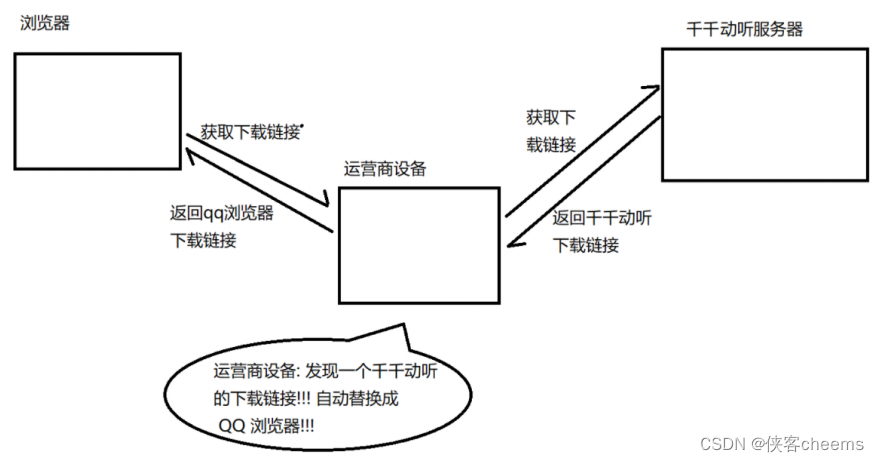
所以:因为http的内容是明文传输的,明文数据会经过路由器、wifi热点、通信服务运营商、代理服务器等多个物理节点,如果信息在传输过程中被劫持,传输的内容就完全暴露了。劫持者还可以篡改传输的信息且不被双方察觉,这就是中间人攻击,所以我们才需要对信息进行加密。
在互联网上, 明文传输是比较危险的事情!!!
HTTPS 就是在 HTTP 的基础上进行了加密, 进⼀步的来保证用户的信息安全~
常见的加密方式
对称加密
- 采用单钥密码系统的加密方法,同一个密钥可以同时用作信息的加密和解密,这种加密方法称为对称加密,也称为单密钥加密,特征:加密和解密所用的密钥是相同的
- 常见对称加密算法(了解):DES、3DES、AES、TDEA、Blowfish、RC2等
- 特点:算法公开、计算量小、加密速度快、加密效率高对称加密其实就是通过同一个"密钥",把明文加密成密文,并且也能把密文解密成明文。
比如下面这种就是对称加密:

非对称加密
- 需要两个密钥来进行加密和解密,这两个密钥是公开密钥(public key,简称公钥)和私有密钥(private key,简称私钥)。
- 常见非对称加密算法(了解):RSA,DSA,ECDSA
- 特点∶算法强度复杂、安全性依赖于算法与密钥但是由于其算法复杂,而使得加密解密速度没有对称加密解密的速度快。
非对称加密要用到两个密钥,一个叫做"公钥",一个叫做"私钥"。
公钥和私钥是配对的,最大的缺点就是运算速度非常慢,比对称加密要慢很多。
- 通过公钥对明文加密,变成密文;通过私钥对密文解密,变成明文(也可以反着用)
- 通过私钥对明文加密,变成密文;通过公钥对密文解密,变成明文
数据摘要&&数据指纹
- 数字指纹(数据摘要),其基本原理是利用单向散列函数(Hash函数)对信息进行运算,生成一串固定长度的数字摘要。数字指纹并不是一种加密机制,但可以用来判断数据有没有被窜改。
- 摘要常见算法:有MD5、SHA1、SHA256、SHA512等,算法把无限的映射成有限,因此可能会有碰撞(两个不同的信息,算出的摘要相同,但是概率非常低)
- 摘要特征:和加密算法的区别是,摘要严格意义不是加密,因为没有解密,只不过从摘要很难反推原信息,通常用来进行数据对比

HTTPS 的工作过程探究
既然要保证数据安全,就需要进行"加密"。
网络传输中不再直接传输明文了,而是加密之后的"密文"。
加密的方式有很多,但是整体可以分成两大类:对称加密和非对称加密
方案1-只使用对称加密
如果通信双方都各自持有同一个密钥X,且没有别人知道,这两方的通信安全当然是可以被保证的(除非密钥被破解)
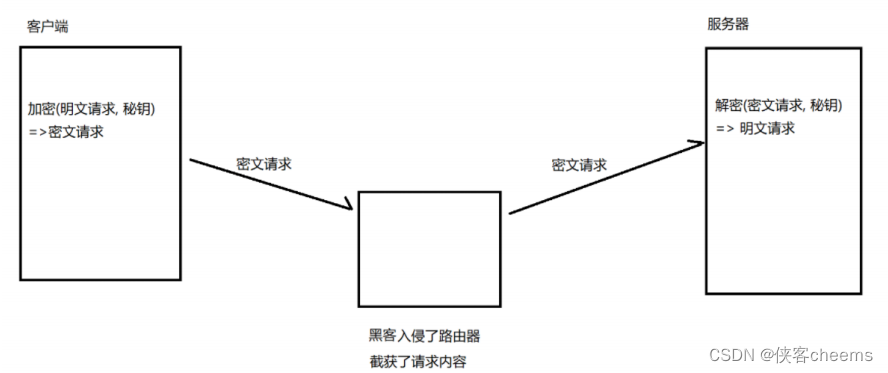
引入对称加密之后,即使数据被截获,由于黑客不知道密钥是啥,因此就无法进行解密,也就不知道请求的真实内容是啥了。
但事情没这么简单。服务器同一时刻其实是给很多客户端提供服务的。这么多客户端,每个人用的秘钥都必须是不同的(如果是相同那密钥就太容易扩散了,黑客就也能拿到了)。因此服务器就需要维护每个客户端和每个密钥之间的关联关系,这也是个很麻烦的事情~
比较理想的做法,就是能在客户端和服务器建立连接的时候,双方协商确定这次的密钥是啥。
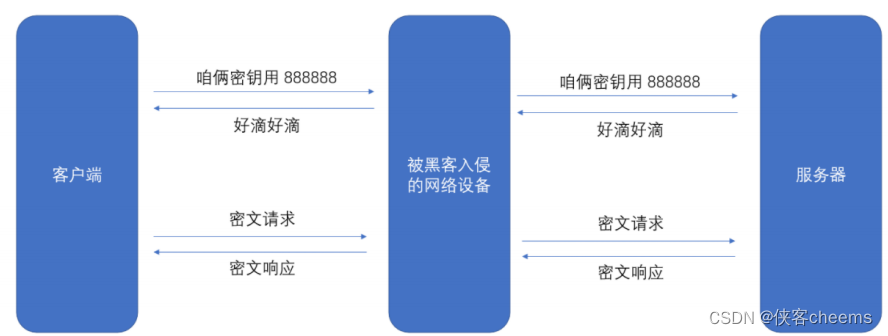
但是我们在正常网络通信时,一般难以直接双方协定固定密钥,所以我们需要将密钥也通过网络传输过去,但是如果直接把密钥明文传输,那么黑客也就能获得密钥了。此时后续的加密操作就形同虚设了。因此密钥的传输也必须加密传输!
但是要想对密钥进行对称加密,就仍然需要先协商确定一个"密钥的密钥"。这就成了"先有鸡还是先有蛋"的问题了,此时密钥的传输再用对称加密就行不通了。
方案2-只使用非对称加密
鉴于非对称加密的机制,如果服务器先把公钥以明文方式传输给浏览器,之后浏览器向服务器传数据前都先用这个公钥加密好再传,从客户端到服务器信道似乎是安全的(有安全问题),因为只有服务器有相应的私钥能解开公钥加密的数据。
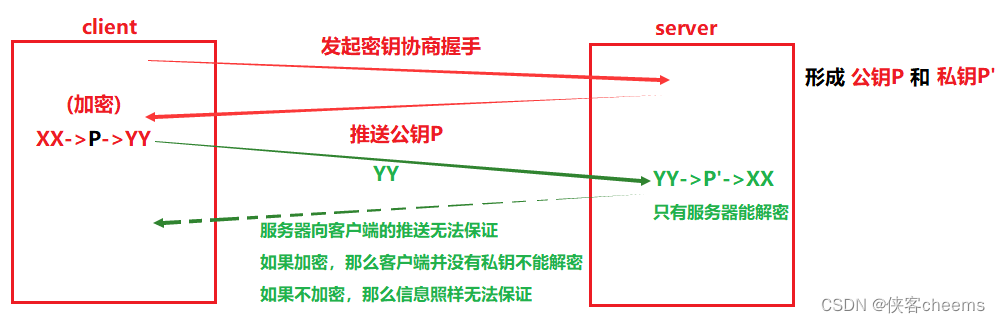
但是服务器到浏览器的这条路怎么保障安全?
如果服务器用它的私钥加密数据传给浏览器,那么浏览器用公钥可以解密它,而这个公钥是一开始通过明文传输给浏览器的,若这个公钥被中间人劫持到了,那他也能用该公钥解密服务器传来的信息。
方案3-双方都使用非对称加密
- 服务端拥有公钥S与对应的私钥S’,客户端拥有公钥C与对应的私钥C’
- 客户和服务端交换公钥
- 客户端给服务端发信息:先用S对数据加密,再发送,只能由服务器解密,因为只有服务器有私钥
- 服务端给客户端发信息∶先用C对数据加密,在发送,只能由客户端解密,因为只有客户端有私钥C’
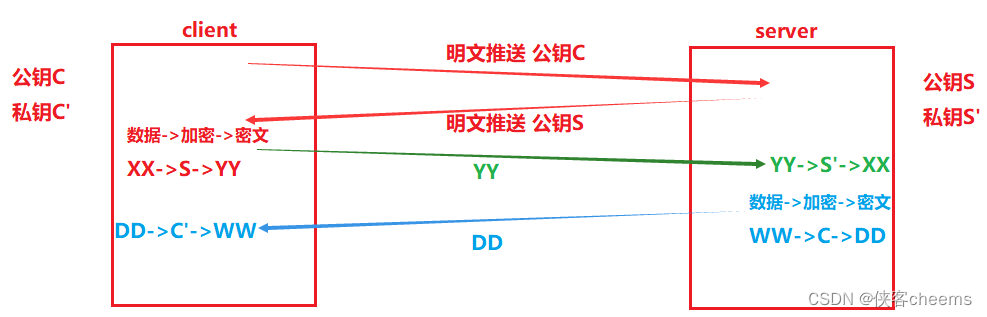
这样貌似也行啊,但是效率太低依旧有安全问题
方案4-非对称加密+对称加密
- 服务端具有非对称公钥S和私钥S’
- 客户端发起https请求,获取服务端公钥S
- 客户端在本地生成对称密钥C,通过公钥S加密,发送给服务器。
- 由于中间的网络设备没有私钥,即使截获了数据,也无法还原出内部的原文,也就无法获取到对称密钥(真的吗?)
- 服务器通过私钥S’解密,还原出客户端发送的对称密钥C。并且使用这个对称密钥加密给客户端返回的响应数据。

方案2,方案3,方案4都存在一个问题,如果最开始,中间人就已经开始攻击了呢?

中间人攻击-针对上面的场景
Man-in-the-MiddleAttack,简称“MITM攻击”
确实,在方案2/3/4中,客户端获取到公钥S之后,对客户端形成的对称秘钥X用服务端给客户端的公舒S进行加密,中间人即使窃取到了数据,此时中间人确实无法解出客户端形成的密钥X,因为只有服务器有私钥S’
但是中间人的攻击,如果在最开始握手协商的时候就进行了,那就不一定了,假设hacker已经成功成为中间人
- 服务器具有非对称加密算法的公钥S,私钥S’
- 中间人具有非对称加密算法的公钥M,私钥M’
- 客户端向服务器发起请求,服务器明文传送公钥S给客户端
- 中间人劫持数据报文,提取公钥S并保存好,然后将被劫持报文中的公钥S替换成为自己的公钥M,并将伪造报文发给客户端
- 客户端收到报文,提取公钥M(自己当然不知道公钥被更换过了),自己形成对称秘钥C,用公钥M加密C,形成报文X发送给服务器
- 中间人劫持后,直接用自己的私钥M’进行解密,得到通信秘钥C,再用曾经保存的服务端公钥S加密后,将报文推送给服务器
- 服务器拿到报文,用自己的私钥S’解密,得到通信秘钥C
- 双方开始采用X进行对称加密,进行通信。但是一切都在中间人的掌握中,劫持数据,进行窃听甚
问题本质出在哪里了呢?客户端无法确定收到的含有公钥的数据报文,就是目标服务器发送过来的!
CA认证
服务端在使用HTTPS前,需要向CA机构申领一份数字证书,数字证书里含有证书申请者信息、公钥信息等。服务器把证书传输给浏览器,浏览器从证书里获取公钥就行了,证书就如身份证,证明服务端公钥的权威性
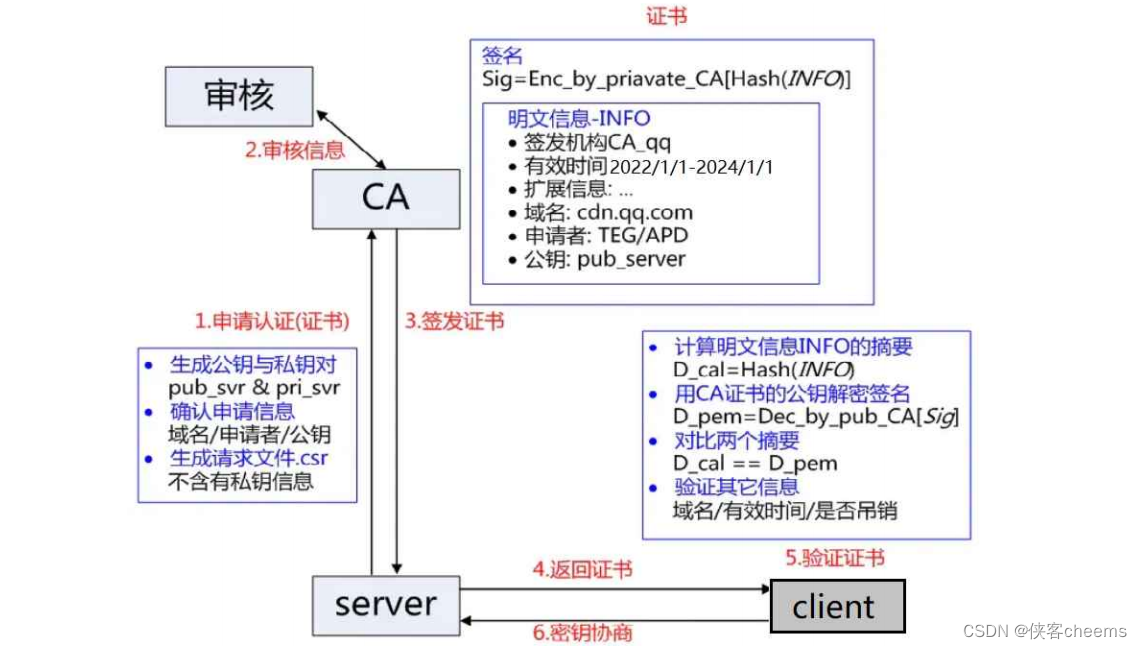
这个证书可以理解成是一个结构化的字符串,里面包含了以下信息:证书发布机构、证书有效期、公钥、证书所有者、签名…
需要注意的是:申请证书的时候,需要在特定平台生成查,会同时生成一对儿密钥对儿,即公钥和私钥。这对密钥对儿就是用来在网络通信中进行明文加密以及数字签名的。
其中公钥会随着CSR文件,一起发给CA进行权威认证,私钥服务端自己保留,用来后续进行通信(其实主要就是用来交换对称秘钥)
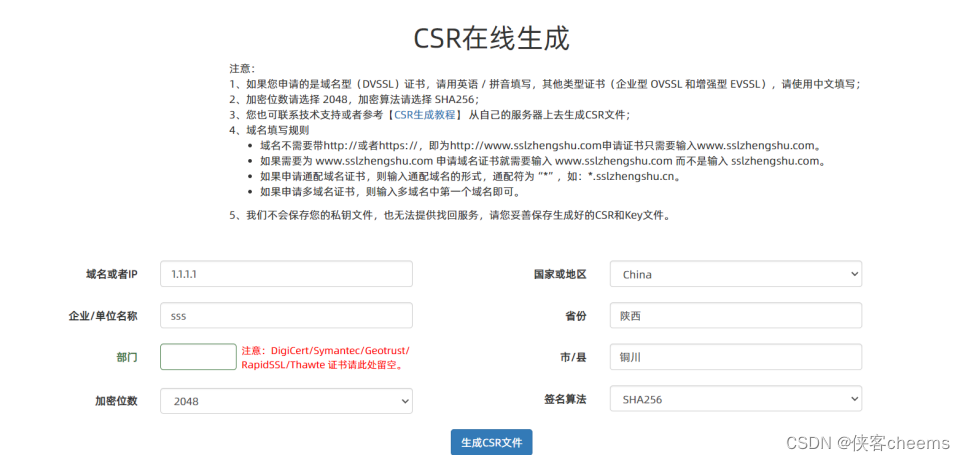
形成CSR之后,后续就是向CA进行申请认证,不过一般认证过程很繁琐,网络各种提供证书申请的服务商,一般真的需要,直接找平台解决就行
理解数据签名
签名的形成是基于非对称加密算法的,注意,目前暂时和https没有关系,不要和https中的公钥私钥搞混了
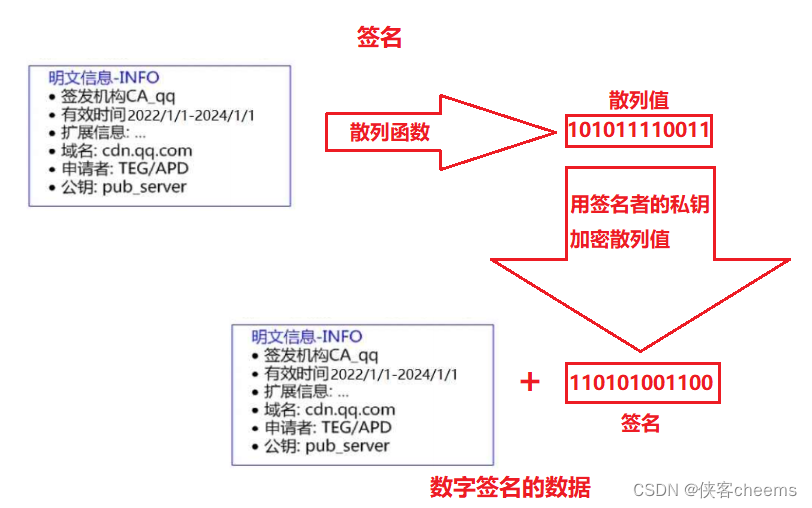
因为我们使用CA的私钥进行形成数据签名,所以,只有CA能形成可信任的证书!
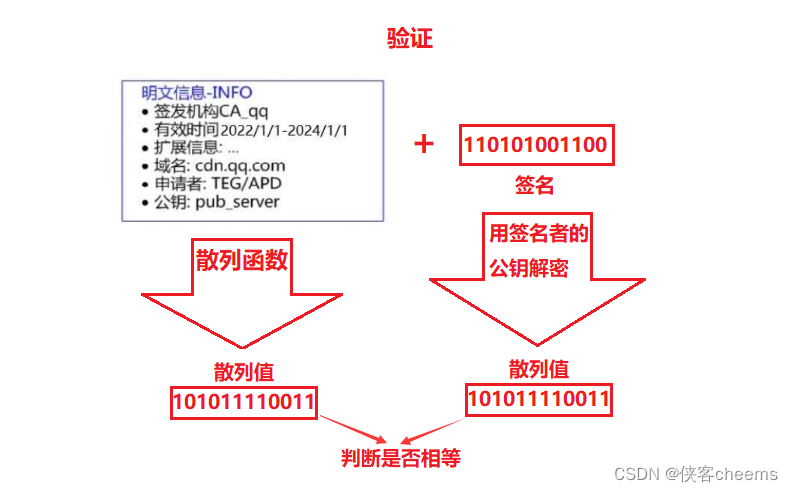
CA会在所有的浏览器中内置自己的公钥,对CA曾经的数据签名进行解密。中间人没有任何办法进行任何局部的替换,无论是明文还是签名。
当服务端申请CA证书的时候,CA机构会对该服务端进行审核,并专门为该网站形成数字签名,过程如下:
- CA机构拥有非对称加密的私钥A和公钥A’
- CA机构对服务端申请的证书明文数据进行hash,形成数据摘要
- 然后对数据摘要用CA私钥A’加密,得到数字签名S
服务端申请的证书明文和数字签名S共同组成了数字证书,这样一份数字证书就可以颁发给服务端了
方案5-非对称加密+对称加密+证书认证
在客户端和服务器刚一建立连接的时候,服务器给客户端返回一个证书,证书包含了之前服务端的公钥,也包含了网站的身份信息。

客户端进行认证
当客户端获取到这个证书之后,会对证书进行校验(防止证书是伪造的).
- 判定证书的有效期是否过期
- 判定证书的发布机构是否受信任(操作系统中已内置的受信任的证书发布机构).
- 验证证书是否被篡改:从系统中拿到该证书发布机构的公钥,对签名解密,得到一个hash值(称为数据摘要),设为hash1。然后计算整个证书的hash值,设为 hash2 对比 hash1和 hash2是否相等,如果相等,则说明证书是没有被篡改过的。
中间人有没有可能篡改该证书?
- 中间人篡改了证书的明文
- 由于他没有CA机构的私钥,所以无法hash之后用私钥加密形成签名,那么也就没法办法对篡改后的证书形成匹配的签名
- 如果强行篡改,客户端收到该证书后会发现明文和签名解密后的值不一致,则说明证书已被篡改,证书不可信,从而终止向服务器传输信息,防止信息泄露给中间人
中间人整个掉包证书?
- 因为中间人没有CA私钥,所以无法制作假的证书
- 所以中间人只能向CA申请真证书,然后用自己申请的证书进行掉包
- 这个确实能做到证书的整体掉包,但是别忘记,证书明文中包含了域名等服务端认证信息,如果整体掉包,客户端依旧能够识别出来。
- 永远记住:中间人没有CA私钥,所以对任何证书都无法进行合法修改,包括自己的
常见问题
为什么摘要内容在网络传输的时候一定要加密形成签名?
常见的摘要算法有: MD5和SHA系列
以MD5为例,我们不需要研究具体的计算签名的过程,只需要了解MD5的特点:
- 定长:无论多长的字符串,计算出来的MD5值都是固定长度(16字节版本或者32字节版本)
- 分散:源字符串只要改变一点点,最终得到的MD5值都会差别很大。
- 不可逆:通过源字符串生成MD5很容易,但是通过MD5还原成原串理论上是不可能的。
正因为MD5有这样的特性,我们可以认为如果两个字符串的MD5值相同,则认为这两个字符串相同。理解判定证书篡改的过程(这个过程就好比判定这个身份证是不是伪造的身份证)
假设我们的证书只是一个简单的字符串 hello,对这个字符串计算hash值(比如md5),结果为BC4B2A76B9719D91
如果hello中有任意的字符被篡改了,比如变成了hella,那么计算的md5值就会变化很大BDBD6F9CF51F2FD8
然后我们可以把这个字符串 hello和哈希值BC4B2A76B9719D91从服务器返回给客户端,此时客户端如何验证hello是否是被篡改过?
那么就只要计算hello 的哈希值,看看是不是BC4B2A76B9719D91即可。
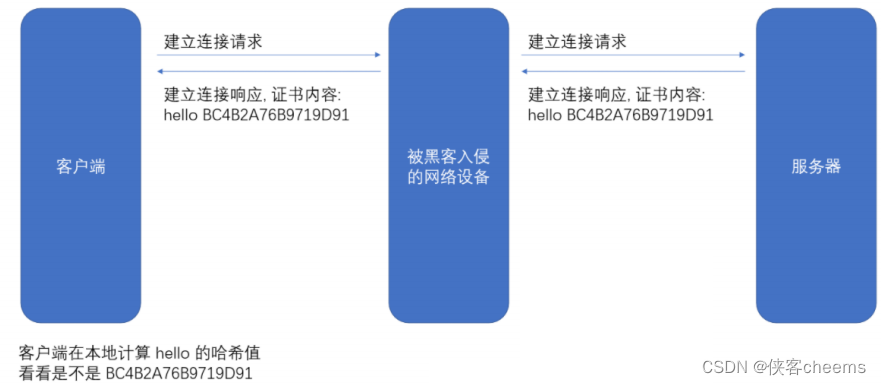
但是还有个问题,如果黑客把 hello篡改了,同时也把哈希值重新计算下,客户端就分辨不出来了呀。
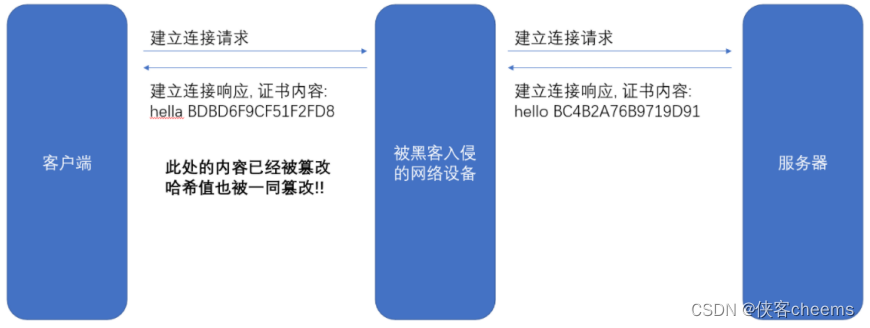
所以被传输的哈希值不能传输明文,需要传输密文。
所以,对证书明文(这里就是“hello”)hash形成散列摘要,然后CA使用自己的私钥加密形成签名,将hello和加密的签名合起来形成CA证书,颁发给服务端,当客户端请求的时候,就发送给客户端,中间人截获了,因为没有CA私钥,就无法更改或者整体掉包,就能安全的证明,证书的合法性。
最后,客户端通过操作系统里已经存的了的证书发布机构的公钥进行解密,还原出原始的哈希值,再进行校验.
为什么签名不直接加密,而是要先hash形成摘要?、
缩小签名密文的长度,加快数字签名的验证签名的运算速度
完整流程
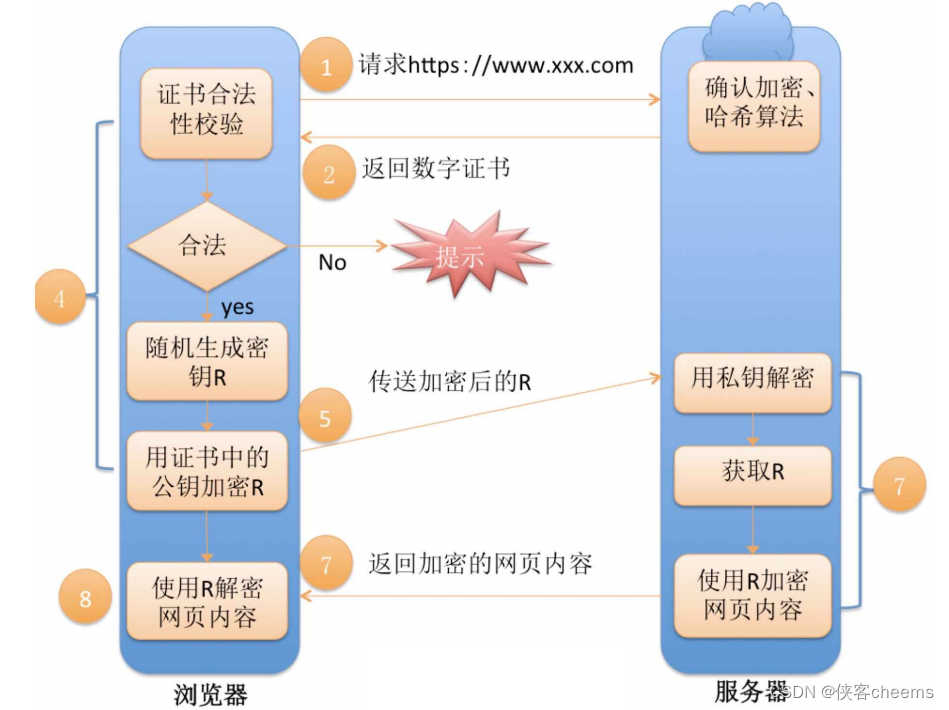
总结
HTTPS工作过程中涉及到的密钥有三组:
- 第一组(非对称加密):用于校验证书是否被篡改,服务器持有私钥(私钥在形成CSR文件与申请证书时获得),客户端持有公钥(操作系统包含了可信任的CA认证机构有哪些,同时持有对应的公钥)。服务器在客户端请求是,返回携带签名的证书。客户端通过这个公钥进行证书验证,保证证书的合法性,进一步保证证书中携带的服务端公钥权威性。
- 第二组(非对称加密):用于协商生成对称加密的密钥。客户端用收到的CA证书中的公钥(是可被信任的)给随机生成的对称加密的密钥加密,传输给服务器,服务器通过私钥解密获取到对称加密密钥。
- 第三组(对称加密):客户端和服务器后续传输的数据都通过这个对称密钥加密解密。
其实一切的关键都是围绕这个对称加密的密钥。其他的机制都是辅助这个密钥工作的。
第二组非对称加密的密钥是为了让客户端把这个对称密钥传给服务器。
第一组非对称加密的密钥是为了让客户端拿到第二组非对称加密的公钥.
如有错误或者不清楚的地方欢迎私信或者评论指出🚀🚀
