免费申请网站com域名设计说明500字通用
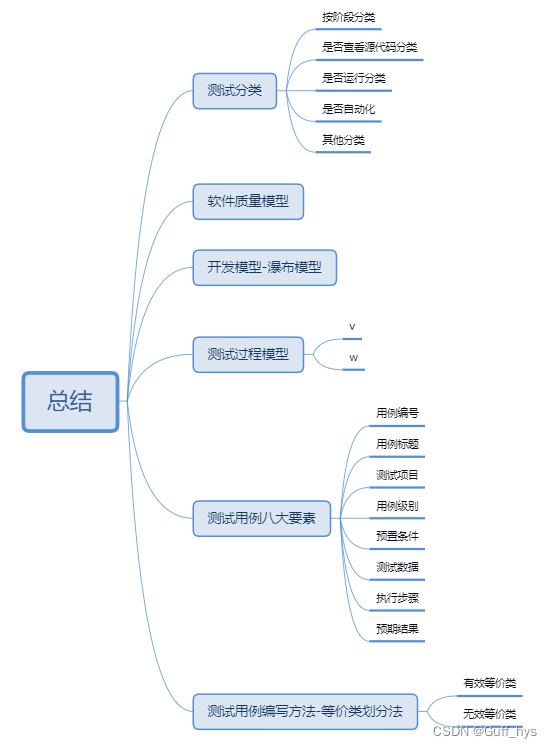
- 软件测试------按测试阶段划分有几个阶段?
单元测试、集成测试、系统测试、验收测试
- 软件测试------按是否查看源代码划分有几种测试方法?
黑盒、白盒、灰盒
- 软件测试------按是否运行划分有几种测试方法?
静态测试、动态测试
- 软件测试------按是否自动化划分有几种测试方法?
手工测试、自动化测试
- 什么是冒烟测试?
对软件最基本的流程和工作做一个粗略的测试, 看最基本的流程是否能跑通 测试拿到研发的第一个版本,一般先冒烟
- 什么是回归测试?
当修复一个bug后,把之前测试用例在新的代码下进行再次测试
- 什么是随机测试?
针对软件中的重要功能进行复测
- 什么是探索性测试?
一边了解和学习项目,一边测试项目
