网站制作预付款会计分录大数据培训机构排行榜
1.思科网络学院
免费学习skillsforall的课程
课程链接:Introduction to Cybersecurity by Cisco: Free Online Course (skillsforall.com)
2.斯坦福大学计算机和网络安全基础
该证书对于初学者来说最有价值,它由最著名的大学之一斯坦福大学提供。您可以免费学习它。它提供了有关安全基础知识、计算机网络及其执行方式的基本概念。
课程链接:Cybersecurity Courses and Programs | Stanford Online
3.国家网络安全职业和研究倡议(NICCS)
美国网络安全和基础设施安全局负责管理 NICCS。他们提供了很多很多学习网络安全的资源,并且分别为大学生和教师提供培训。
课程链接:One Million Certified in Cybersecurity – Free ISC2 Certification Exams

4.Microsoft Learn 安全认证
这是网络安全最有价值的证书之一。它由 Microsoft 提供,您可以通过 Microsoft Learn 网站访问它。他们免费提供大量的认证。
课程链接:Microsoft Certified: Cybersecurity Architect Expert - Certifications | Microsoft Learn
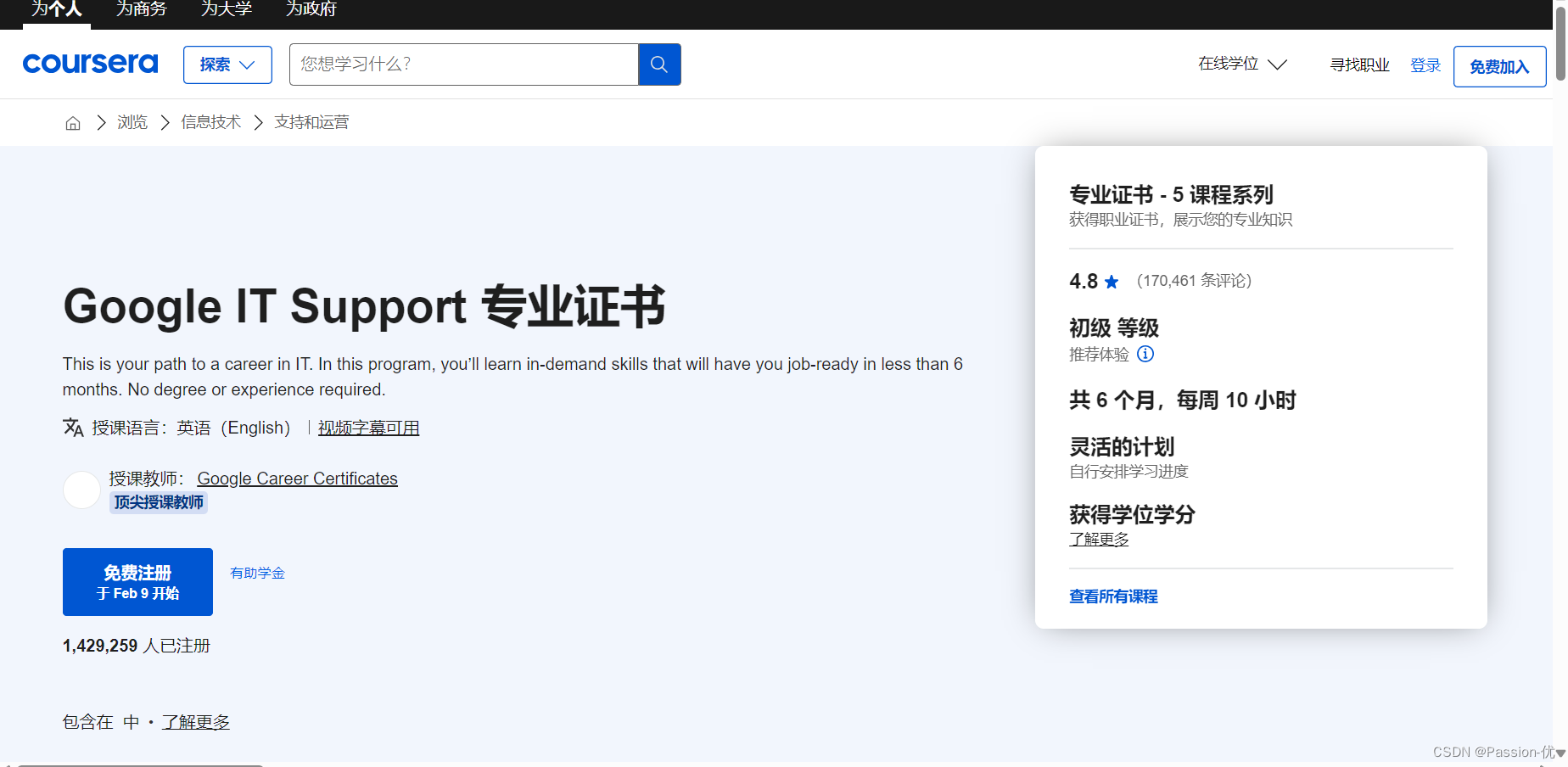
5.Google IT支持专业证书
这是您最喜欢的认证之一,来自一家您可以认出的最喜欢的公司。谷歌通过 Coursera 平台提供它。他们还在 Coursera 平台上提供网络安全基础课程。Google 员工是这些课程的讲师。
课程链接:Google IT Support 专业证书 | Coursera
6.EC 理事会的基本系列
它是 EC 理事会通过编码平台提供的网络安全领域最有价值的课程之一。它有很多深入的课程,不仅有安全课程,还有数字取证课程、网络基础课程、Python 课程。
课程链接:Home page | EC-Council Learning (eccouncil.org)