郑州正规的网站制作价钱外观设计公司
文章目录
- 前言
- 1. 编写MENJA小游戏
- 2. 安装cpolar内网穿透
- 3. 配置MENJA小游戏公网访问地址
- 4. 实现公网访问MENJA小游戏
- 5. 固定MENJA小游戏公网地址
前言
本篇教程,我们将通过VS Code实现远程开发MENJA小游戏,并通过cpolar内网穿透发布到公网,分享给无论身在何地的好友体验由你开发的游戏的乐趣。
话不多说,下面就来教大家如何使用VS Code编写一个MENJA切块小游戏,这里我们使用VS Code并结合Live Server插件进行调试,Live Server可以实现一键安装,实现自动刷新,架设本地服务器环境。
1. 编写MENJA小游戏
本篇文章的小游戏源代码地址:https://github.com/ADAMxWANG/menja
下载ZIP压缩包到本地:
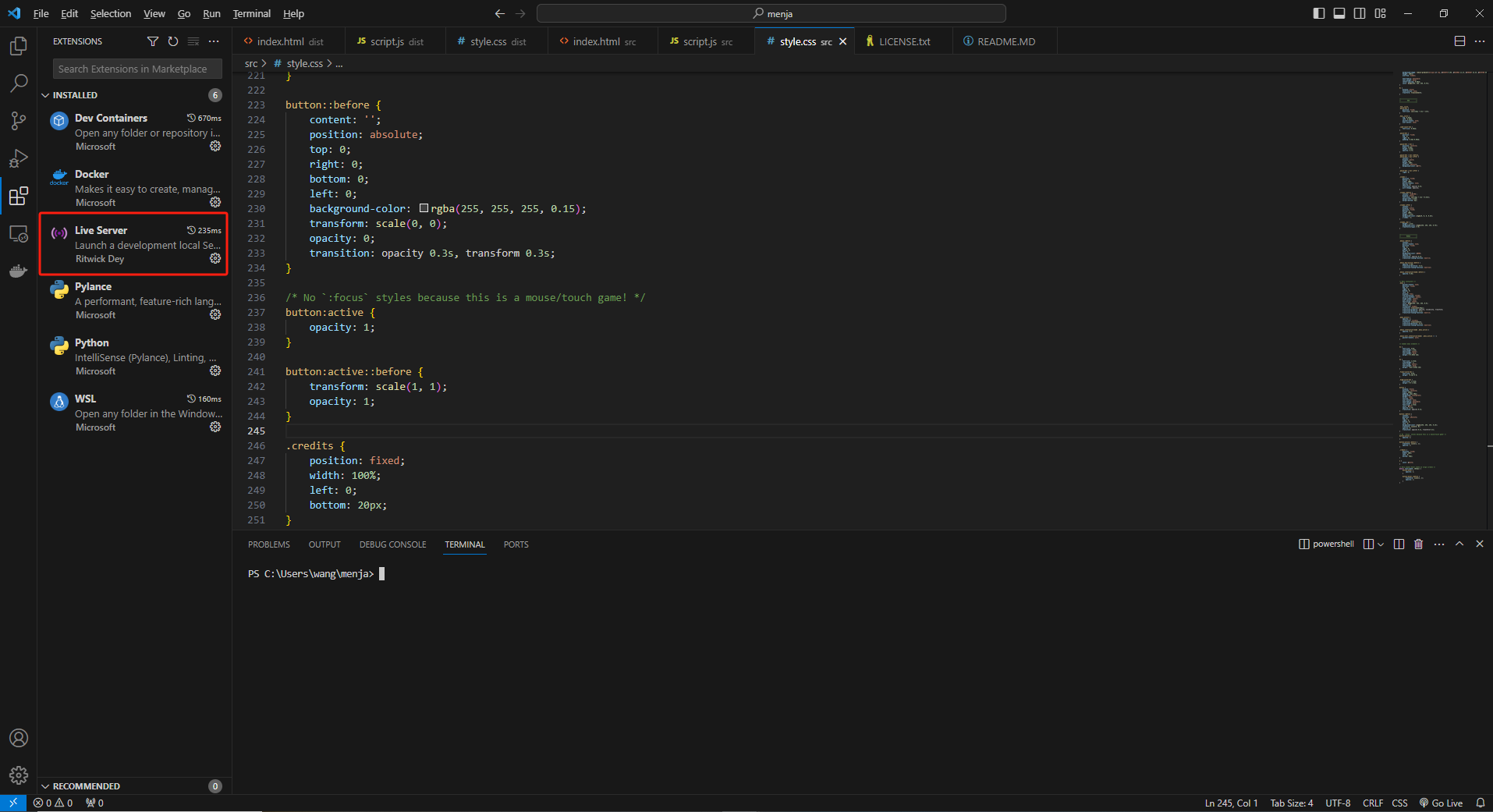
在VS Code扩展中搜索Live Server,并安装
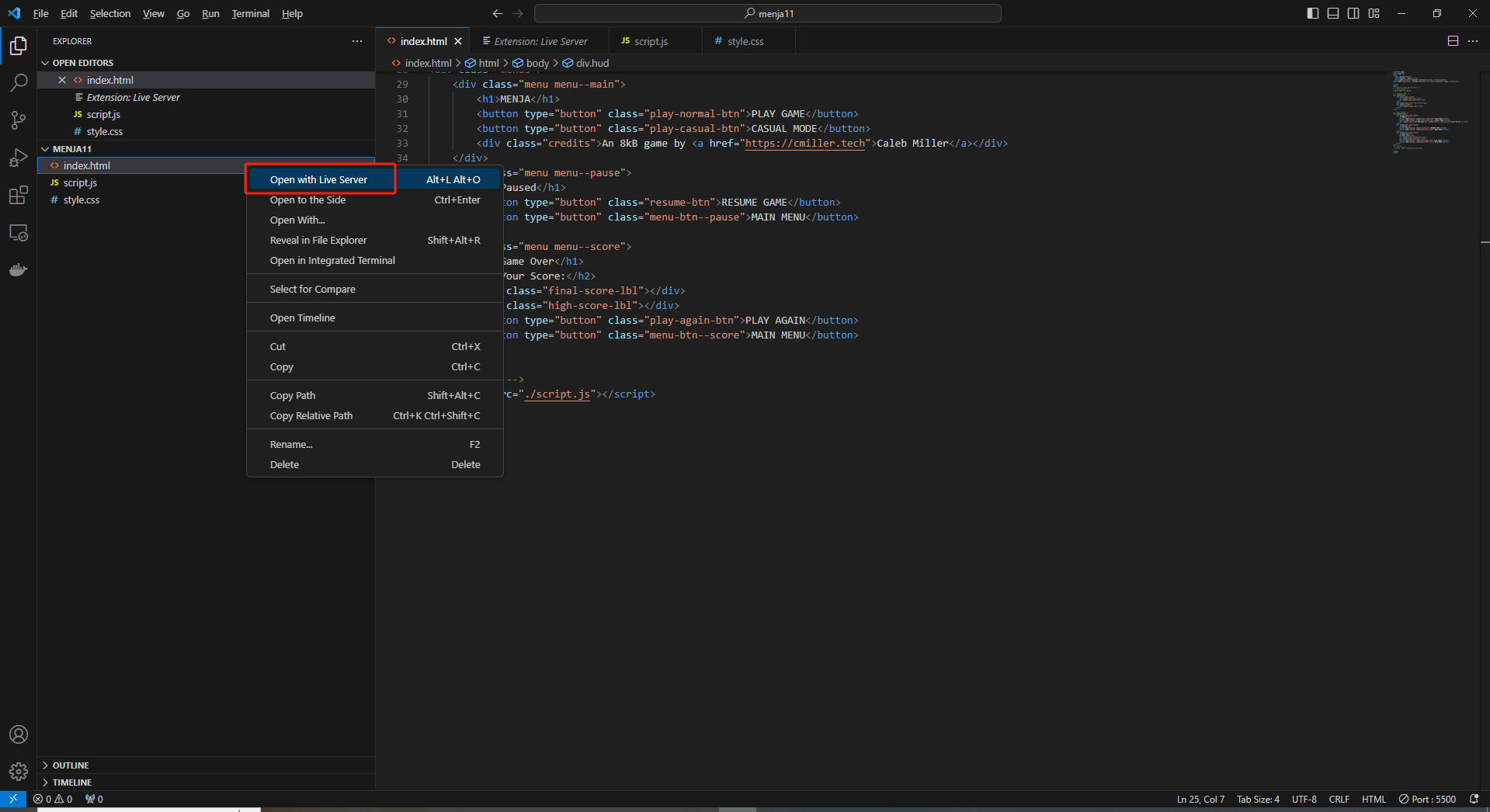
右键index.html文件,点击Open with Live Server 弹出web界面,端口为 5500
接下来可以在menja文件夹下进行调试,并使用Live Server随时进行调试,实时查看开发的网页
接下来我们要把制作好的游戏网页发布至公网,分享给好友访问。
2. 安装cpolar内网穿透
要将游戏分享给好友,首先我们需要在Linux安装cpolar内网穿透工具,通过cpolar 转发本地端口映射的http公网地址,我们可以很容易实现远程访问,而且无需自己注册域名购买云服务器.下面是安装cpolar步骤:
cpolar官网地址: https://www.cpolar.com
- 使用一键脚本安装命令
curl -L https://www.cpolar.com/static/downloads/install-release-cpolar.sh | sudo bash
- 向系统添加服务
sudo systemctl enable cpolar
- 启动cpolar服务
sudo systemctl start cpolar
cpolar安装成功后,在外部浏览器上访问Linux 的9200端口即:【http://局域网ip:9200】,使用cpolar账号登录,登录后即可看到cpolar web 配置界面,结下来在web 管理界面配置即可。
3. 配置MENJA小游戏公网访问地址
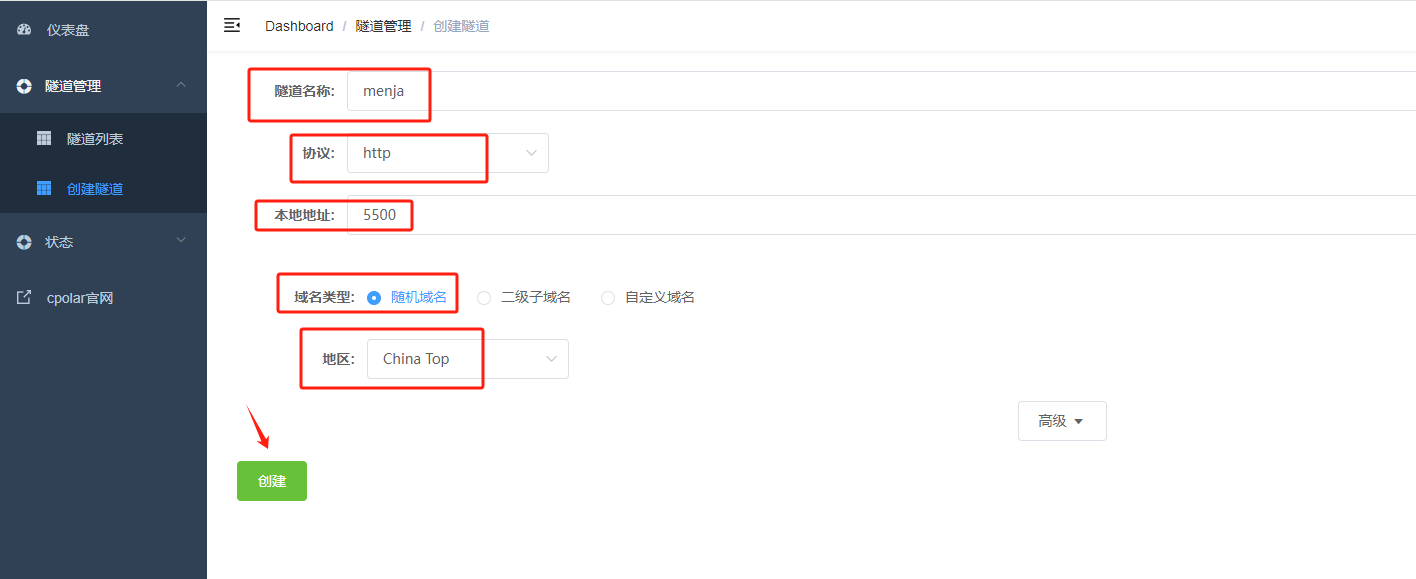
点击左侧仪表盘的隧道管理——创建隧道,创建一个MENJA小游戏的cpolar 公网地址隧道!
- 隧道名称:可自定义命名,注意不要与已有的隧道名称重复
- 协议:选择http
- 本地地址:5500 (本地访问时的端口)
- 域名类型:免费选择随机域名
- 地区:选择China Top
点击创建
隧道创建成功后,点击左侧的状态——在线隧道列表,查看所生成的公网访问地址,有两种访问方式,分别是 http 和 https 。
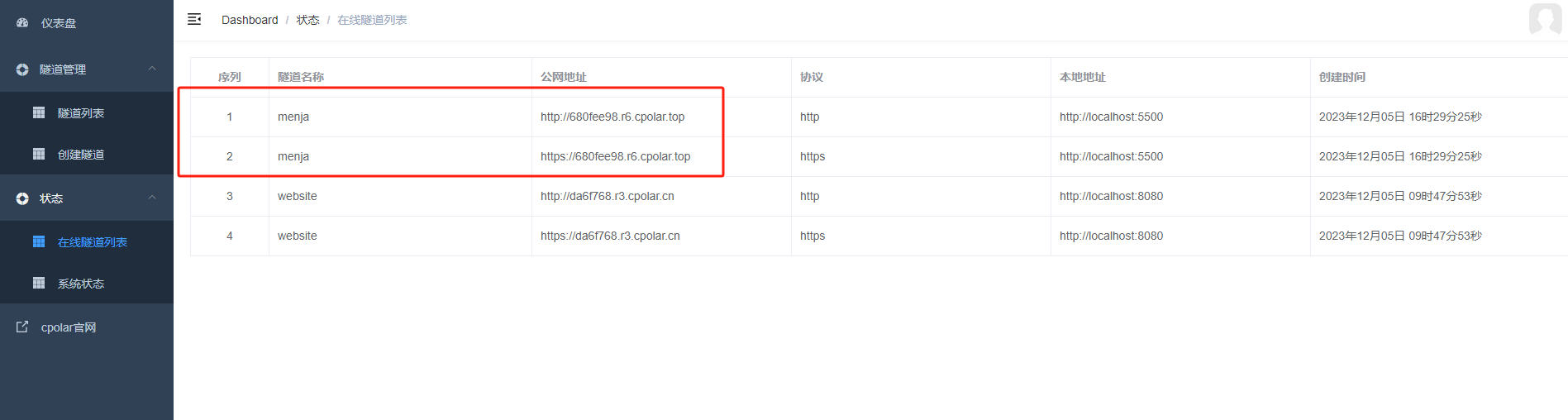
4. 实现公网访问MENJA小游戏
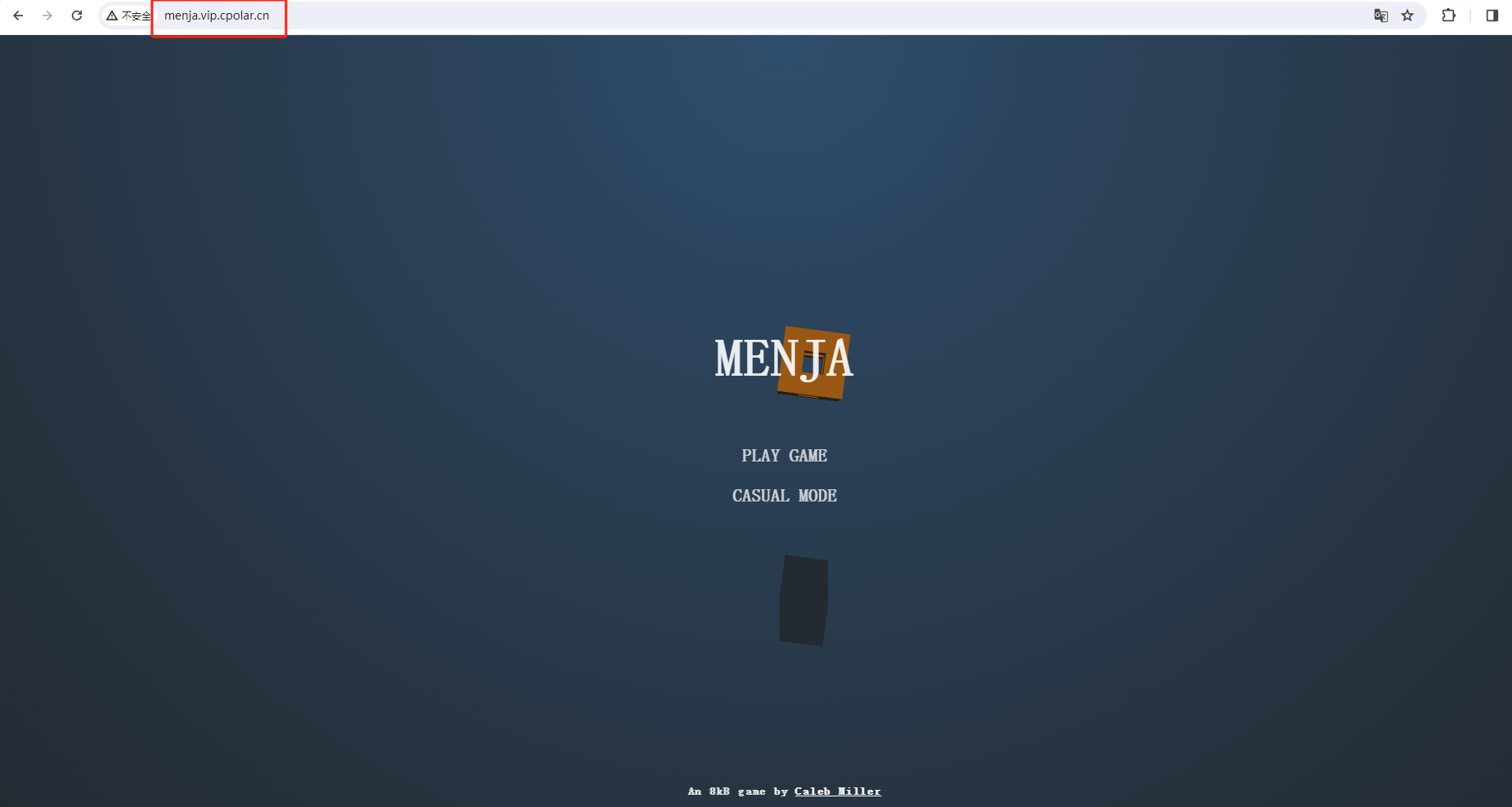
使用上面的cpolar https公网地址,在任意设备的浏览器进行访问,即可成功看到小游戏界面,这样一个公网地址且可以远程访问就创建好了,使用了cpolar的公网域名,无需自己购买云服务器,即可发布到公网随时随地进行远程访问。(Tips:新域名登录,可能需要重新登陆)
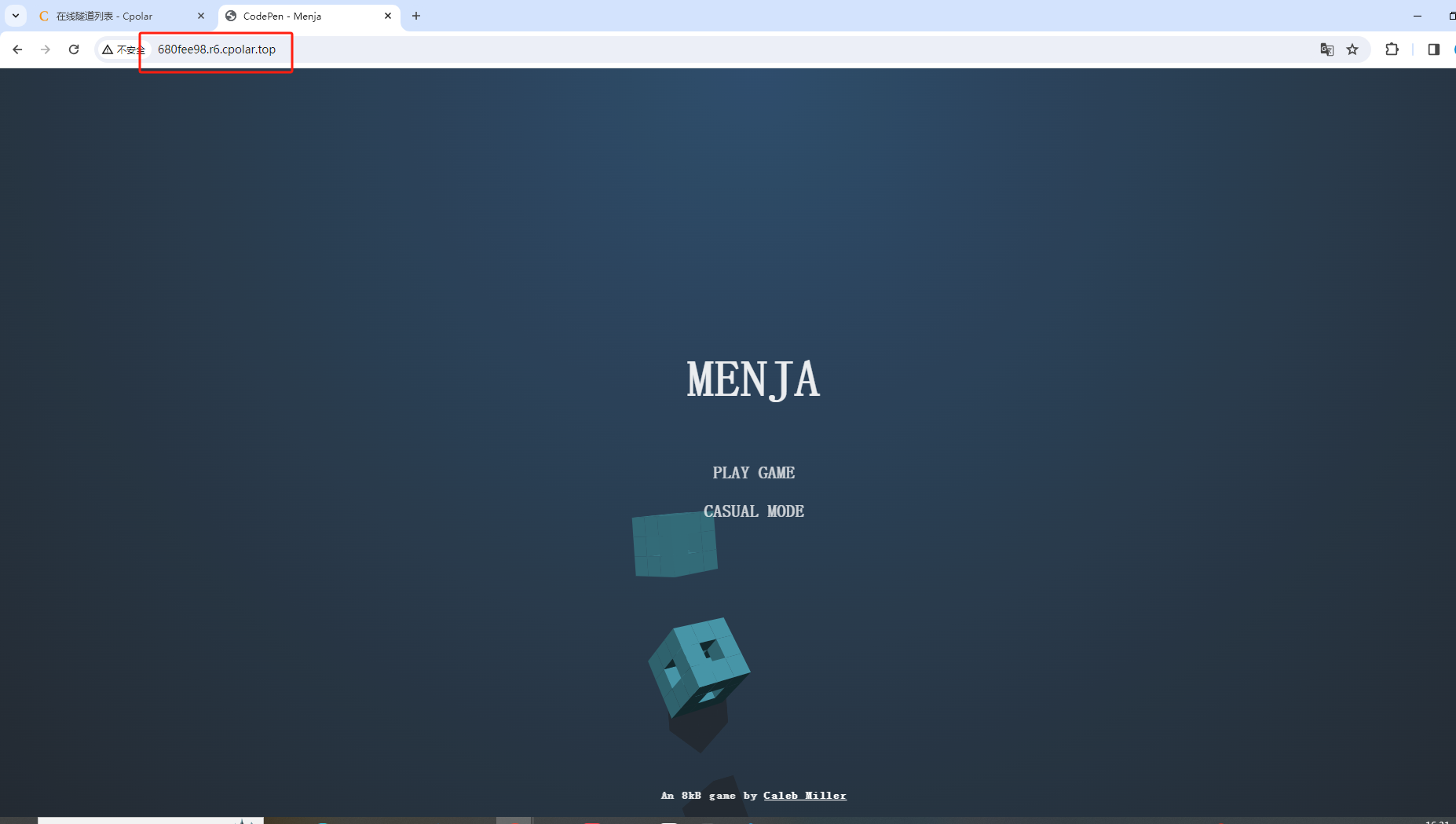
5. 固定MENJA小游戏公网地址
由于以上使用cpolar所创建的隧道使用的是随机公网地址,24小时内会随机变化,不利于长期远程访问。我一般会使用固定二级子域名,因为我希望将游戏网址发送给朋友玩时,可以直接使用简单好记的固定公网地址进行访问,不用每天都更换地址访问,可以一直愉快的享受游戏。
固定二级子域名长这样(例如:MENJA.cpolar.cn),该地址为固定地址,不会随机变化。
注意需要将cpolar套餐升级至基础套餐或以上,且每个套餐对应的带宽不一样。【cpolar.cn已备案】
登录cpolar官网,点击左侧的预留,选择保留二级子域名,设置一个二级子域名名称,点击保留,保留成功后复制保留的二级子域名名称。
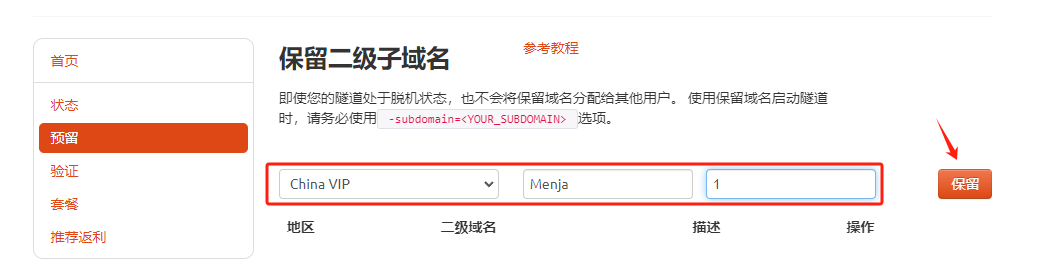
保留成功后复制保留成功的二级子域名的名称
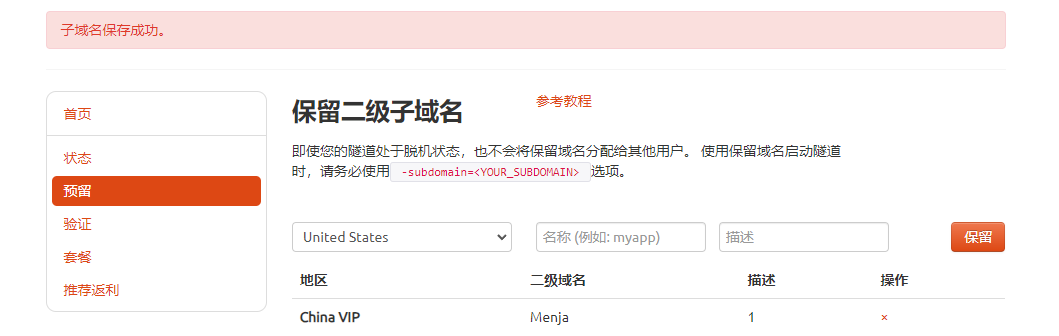
返回登录cpolar web UI管理界面,点击左侧仪表盘的隧道管理——隧道列表,找到所要配置的隧道,点击右侧的编辑
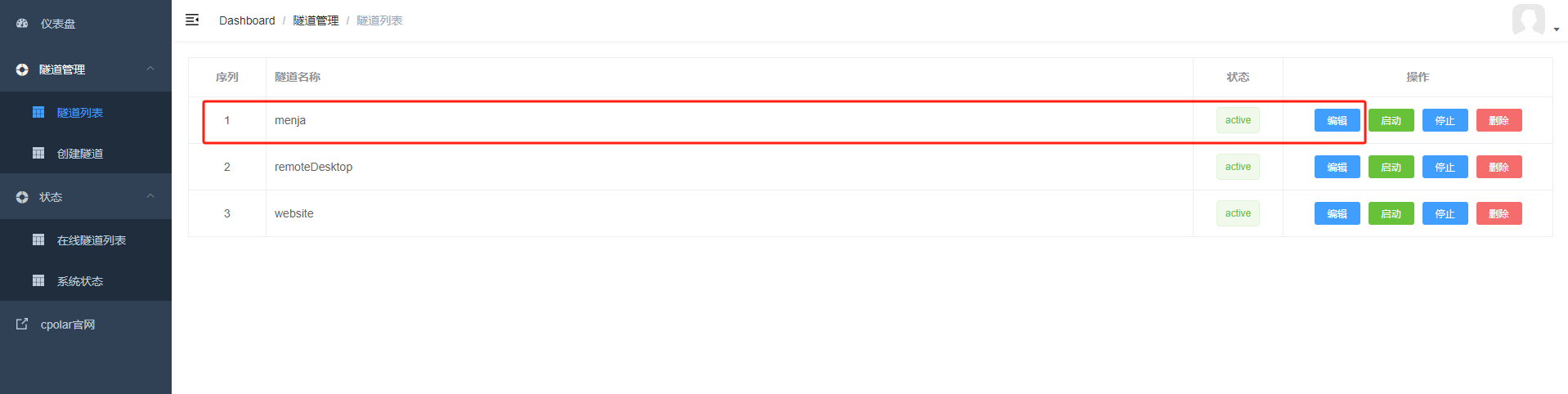
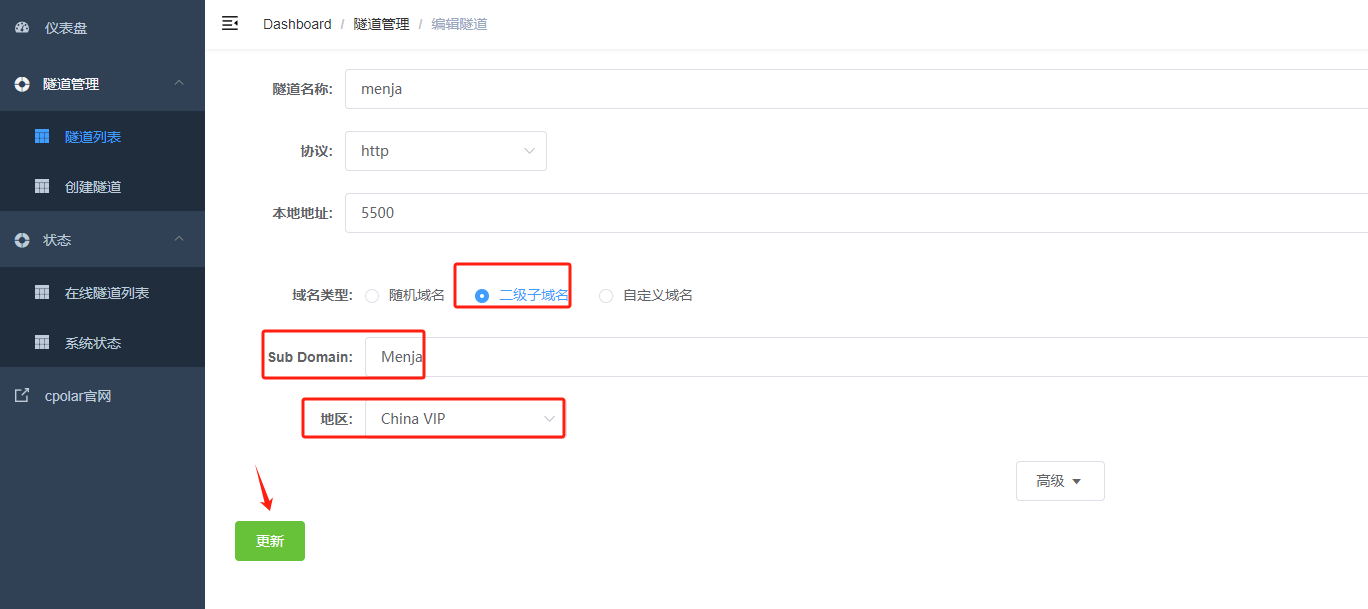
修改隧道信息,将保留成功的二级子域名配置到隧道中
- 域名类型:选择二级子域名
- Sub Domain:填写保留成功的二级子域名
点击更新(注意,点击一次更新即可,不需要重复提交)
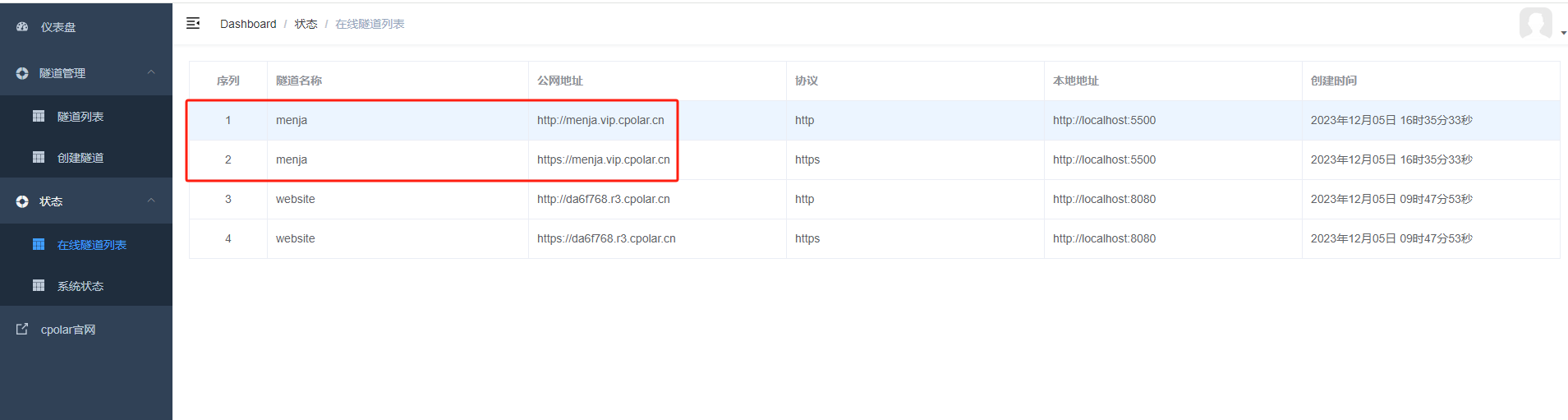
更新完成后,打开在线隧道列表,此时可以看到公网地址已经发生变化,地址名称也变成了固定的二级子域名名称的域名
最后,我们使用固定的公网地址访问游戏网页,可以看到访问成功,这样一个固定且永久不变的公网地址就设置好了。
现在我们可以把这个通过VS Code编写的web网页或者游戏网页,通过cpolar生成的固定地址分享给你的好朋友们随时随地来进行远程游戏啦~