乌兰浩特网站制作网站框架搭建
🕺作者: 主页
我的专栏 C语言从0到1 探秘C++ 数据结构从0到1 探秘Linux 菜鸟刷题集 😘欢迎关注:👍点赞🙌收藏✍️留言
🏇码字不易,你的👍点赞🙌收藏❤️关注对我真的很重要,有问题可在评论区提出,感谢阅读!!!
文章目录
- 实验一 安装和使用Oracle数据库
- 【实验目的】
- 【实验内容】
- 【实验总结】
实验一 安装和使用Oracle数据库
【实验目的】
- 掌握Oracle软件安装过程,选择安装组件
- 掌握建立Oracle数据库,配置网络连接
- 使用SQL*Plus,登录到实例和数据库
- 掌握命令方式的关闭和启动实例及数据库
【实验内容】
- 安装ORACLE
- 第一步:打开安装程序,选择创建配置单实例数据库,注意要在不含中文的目录下,如图1-1所示。
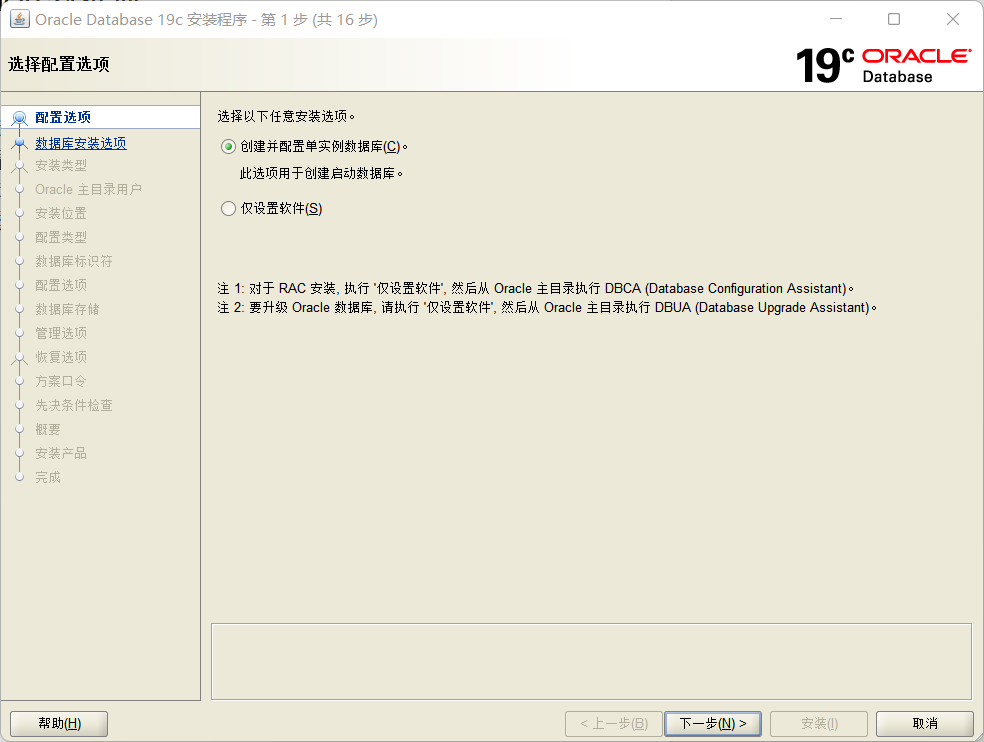
图1-1 选择创建配置单实例数据库
- 第二步:选择桌面类,如图1-2所示。
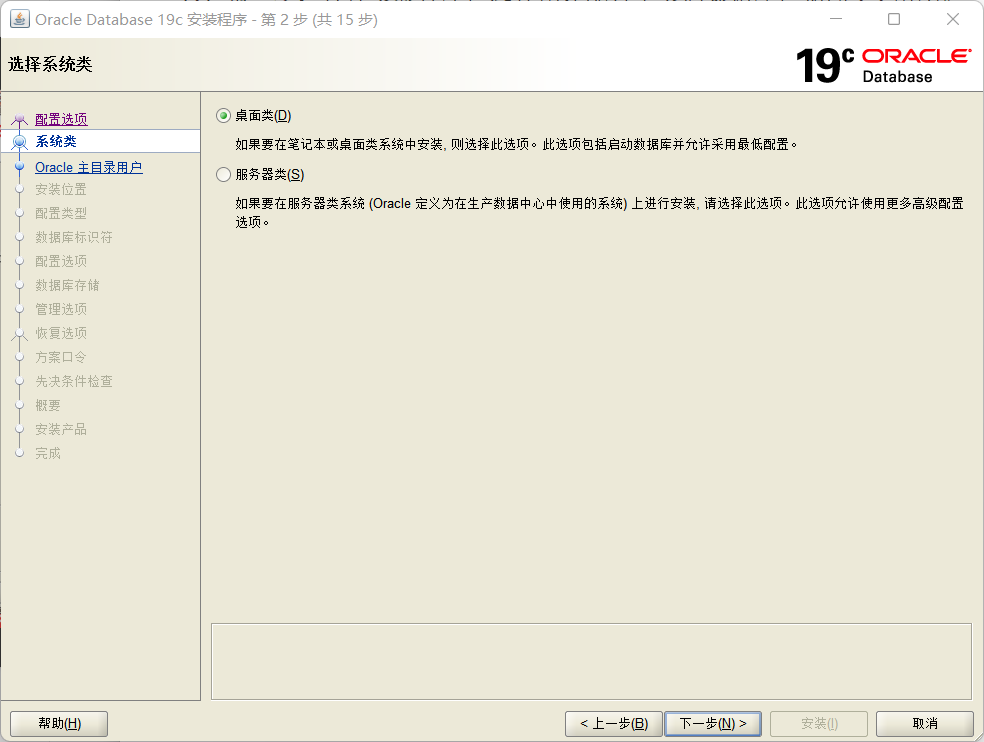
图1-2 选择桌面类
- 第三步:使用虚拟账户,如图1-3所示。
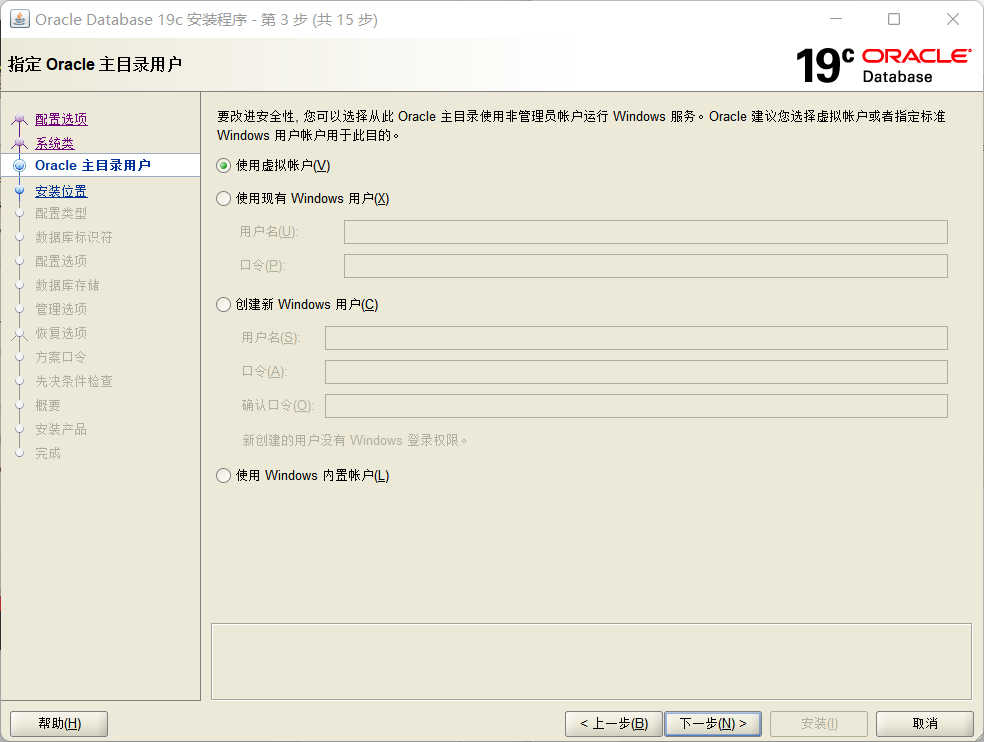
图1-3 使用虚拟账户
- 第四步:进行基本配置,注意目录的格式,如图1-4所示。
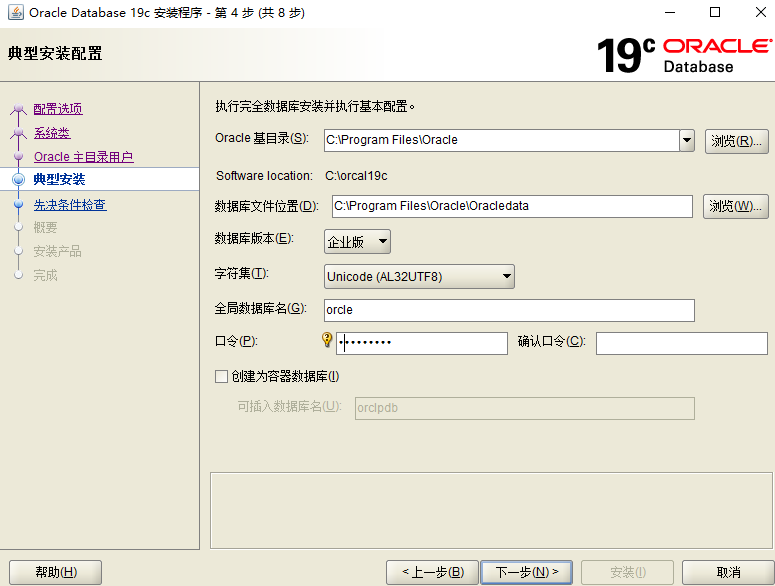
图1-4进行基本配置
- 第五步:执行先决条件检查然后安装,如图1-5所示。
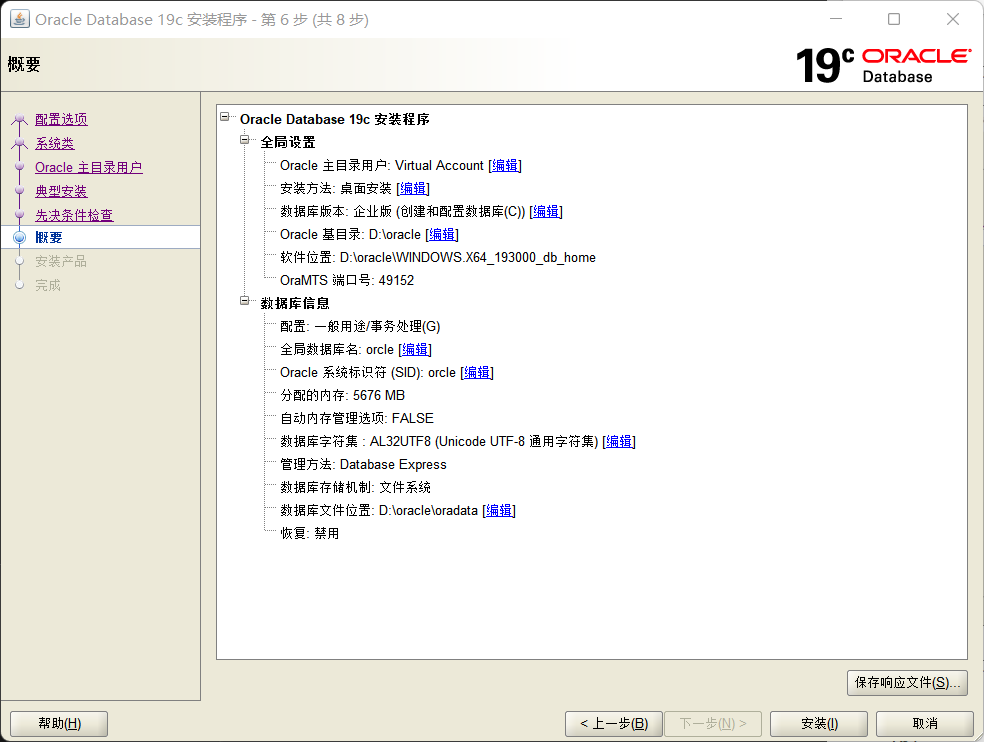
图1-5检查
- 第六步:安装程序,在安装时发现”无法将 NANFANG\nanfang 安装用户添加到 %2% 组。”,此时只需要多点几次“继续”即可,如图1-6所示。

图1-6处理错误
- 第七步:如果显示配置成功则配置成功,如图1-7所示。

图1-7配置成功
- 运行SQL*Plus,分别用SYS和SYSTEM用户名和密码登录,如图1-8、1-9所示。

图1-8使用sys用户
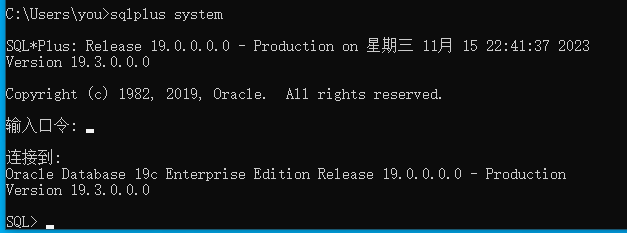
图1-9使用system用户
- 查看服务,记录下和数据库有关的服务名,将他们设为手动方式,启动相关服务,如图1-10所示。

图1-10将服务设置为手动
- 配置监听器,查看是否在服务中有LISTENER,是否能启动,如图1-11所示。

图1-11配置监听器
- 配置本地net服务,提示:设置正确的服务器地址和端口号,如图1-12所示。
先以管理员身份运行Net Configuration Assistant菜单,弹出下图:
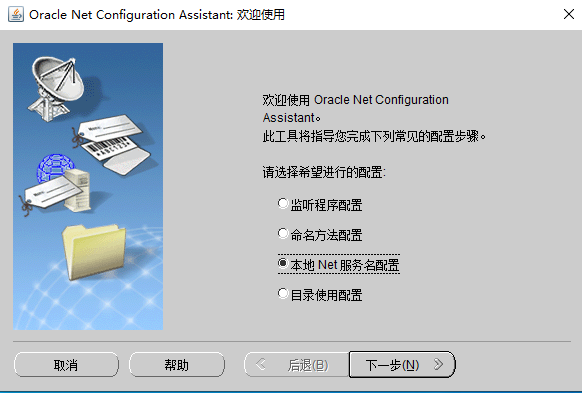
图1-12 选择“本地Net服务名配置”

图1-13选择“添加”
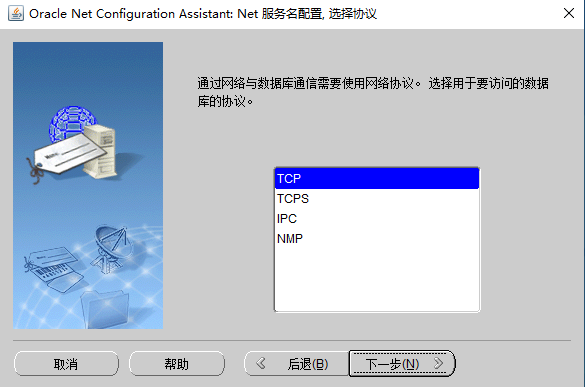
图1-14选择“TCP”
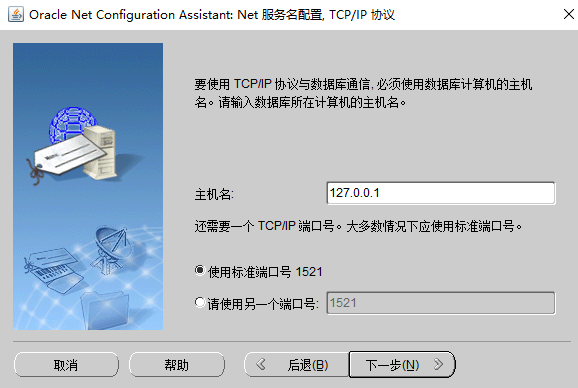
图1-15配置“主机名和端口号”
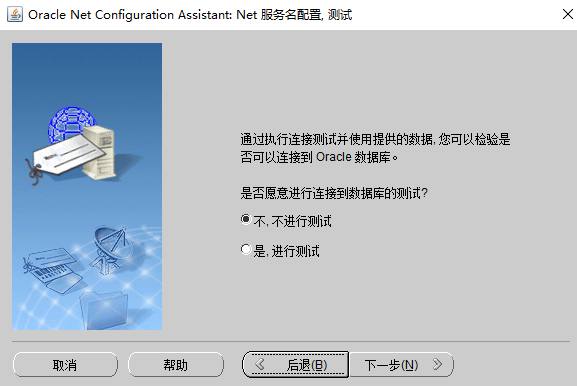
图1-16 选择是否“测试”
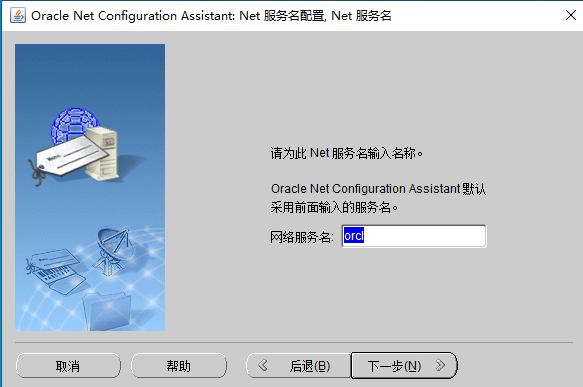
图1-17 配置网络服务名

图1-18配置完毕
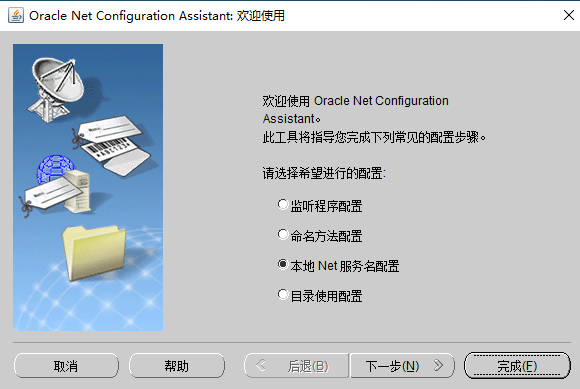
图1-19点击下一步回到首页
- 用system用户测试是否能连接成功,如图1-20所示。

图1-20 测试连接
- 用命令关闭实例和数据库,记录命令,再用命令以NOMOUNT的方式分三步启动实例及数据库:启动实例,再加载数据库,打开数据库。
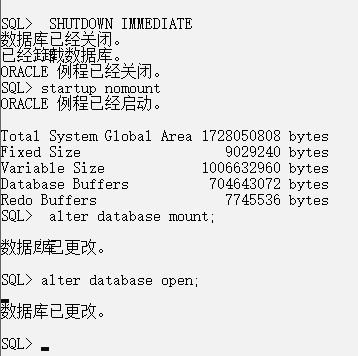
图1-21关闭实例和启动实例
【实验总结】
本次实验的主要目的是学习和掌握安装和使用Oracle数据库的过程。通过实验,我们完成了以下内容:
-
安装Oracle:根据步骤选择创建配置单实例数据库,并进行基本配置。在安装过程中可能会出现一些错误提示,需要多次点击"继续"来解决。最后确认配置成功。
-
使用SQL*Plus登录实例和数据库:我们使用SYS和SYSTEM用户名和密码分别登录到实例和数据库,这样我们可以进一步操作数据库。
-
配置监听器和本地net服务:我们配置了监听器,检查是否有LISTENER服务并启动。然后配置本地net服务,设置正确的服务器地址和端口号,并使用system用户测试连接是否成功。
-
关闭和启动实例及数据库:我们学习了使用命令关闭实例和数据库,并记录了相应的命令。然后以NOMOUNT的方式分三步启动实例及数据库:启动实例、加载数据库和打开数据库。
通过本次实验,我们对Oracle数据库的安装和使用过程有了更深入的了解。掌握了安装组件、建立数据库、配置网络连接、登录实例和数据库、关闭和启动实例及数据库等关键步骤和操作。这些知识对于我们日后的数据库管理和应用开发都具有重要的意义。
