旅游网站制作模板三亚最新通告文昌最新通告
一周新的开始,今天的你学习了吗?
前言
今天打算把数组的相关知识知识复习一下,比如初始化,调用,以及他和指针的关系等等
数组是什么
数组是一种数据结构,它由相同类型的元素组成,并按照一定的顺序排列。每个元素在数组中都有一个唯一的索引,通过索引可以访问和操作数组中的元素。数组可以存储多个值,并且这些值可以是不同的数据类型,例如整数、浮点数、字符等。数组的大小在创建时就确定了,一旦确定就不能改变。
数组的特点
数组的特点是可以通过索引快速访问和修改元素,因为数组中的元素在内存中是连续存储的。数组还可以进行各种操作,如插入、删除、排序等。
一维数组
一维数组的定义
在C语言中,一维数组的构成由数据类型和数组名组合而成。例如,int类型的数组可以定义为int array[5],其中array是数组名,int是数据类型,5是数组的大小,[]是下标引用操作符,这个数组可以存储5个整数值。
int arr[5];
char arr[5];
float arr[5];
一维数组元素的调用与修改
要知道数组每个元素都有对应的下标,从低地址向高地址依次是0,1,2,3……
如图所示(技术不好请多包涵)
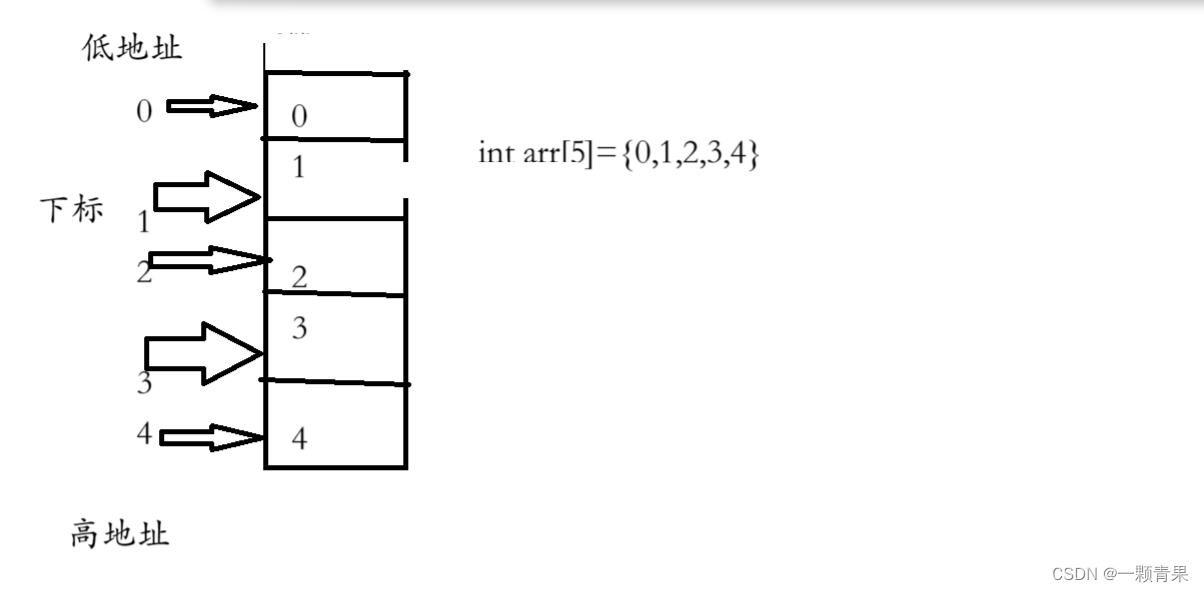
🦊当我们要使用第一个元素时只需要调用下标为0的元素即可

看,第一个元素被打印了出来
🦊如果是要修改也是这样调用
 看,第一个元素被改为了10
看,第一个元素被改为了10
一维数组的初始化
🔊 🔊 🔊完全初始化
给每个元素都赋值
int arr[5] = {1,2,3,4,5};
🔊 🔊 🔊不完全初始化
未被覆盖到的元素默认修改为0
int arr[5] = {1,2,3};
二维数组
二维数组的定义
与一维数组十分相似,
int arr[3][4];
表示创建了一个3行4列的数组,元素是int类型
二维数组元素的调用
😴 🔊如下图所示,直接使用对应下标即可

但是,我们要知道二维数组在内存中存储的空间先线性连续的,
😴 🔊也就是这样
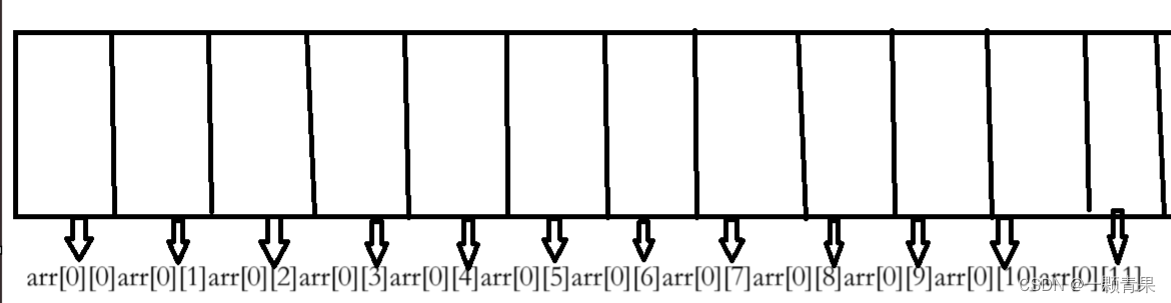
只是调用的时候按照二维来看而已
二维数组的初始化
👻完全初始化
int arr[3][4] = {1,2,3,4,5,6,7,8,9,10,11,12};
int arr[3][4] = { {1,2,3,4},{5,6,7,8},{9,10,11,12} };
第二种完全初始化是每个小括号是一行的元素
👻不完全初始化
int arr[3][4] = {1,2,3,4,5};
int arr[3][4] = { {1,2,3,},{5,6,7,} };
第二种完全初始化是每个小括号是一行的元素
那么问题来了,下面两种写法一样,吗
int arr[3][4] = { 1,2,3,4,5,6 };
int arr[3][4] = { {1,2,3},{4,5,6} };
请看
显然是不一样的,原因刚才也说了小括号里是一行的元素,不够就补零
变长数组
来历
🔊 C99是C语言的一种标准,指的是1999年发布的C语言标准,也被称为ISO/IEC 9899:1999。它是C语言自1989年发布的C89(或ANSI C)标准之后的第二个主要更新版本。C99引入了一些新特性,就包括变长数组。
在c99之前数组大小是用常量指定的,c99后引入了变长数组的概念
变长数组(Variable Length Array,VLA)是一种在创建数组时可以使用变量指定数组长度的数组。与普通数组不同,变长数组的大小在创建后保持不变。变长数组只能是局部变量,并且必须是自动存储类别,不能使用extern或static存储类别说明符。
要说明的是一些IDE不是很好的支持c99,例如vs,他就不能使用变长数组
变长数组的使用
int a;
scanf("%d", &a);
int arr[a];
变长数组的特点
- 变长数组的长度可以使用变量来指定,而不仅限于常量或常量表达式。
- 变长数组不能在定义时进行初始化,需要在运行时动态分配内存。
- 变长数组本质上是静态数组,即数组的长度在变量的整个生命周期中是不可变的。
- 变长数组分配在栈上,因此只能是局部变量。
- 变长数组适用于多维数组。
🔊根本特征
变长数组只有在运行时才可以确定大小,根据变量大小指定元素个数,确定后不在变换。
这里插一嘴,在动态内存分配里有个和它像的东西叫做柔性数组,感兴趣的可以去了解一下。
🦊今天的分享就到这里了,觉得有帮助的话就点个赞支持一下吧!

