重庆网上商城网站建设织梦5.5模版安装上去为什么打开网站图片不能显示教程
一、介绍
本篇文章是介绍的是Python 世界中最火的第三方单元测试框架:pytest。它有如下主要特性:
- assert 断言失败时输出详细信息(再也不用去记忆 self.assert* 名称了)
- 自动发现测试模块和函数
- 模块化夹具用以管理各类测试资源
- 对 unittest 完全兼容,对 nose 基本兼容
- 非常丰富的插件体系,有超过 315 款第三方插件,社区繁荣
和前面介绍 unittest 和 nose 一样,我们将从如下几个方面介绍 pytest 的特性。
二、用例编写
同 nose 一样,pytest 支持函数、测试类形式的测试用例。最大的不同点是,你可以尽情地使用 assert 语句进行断言,丝毫不用担心它会在 nose 或 unittest 中产生的缺失详细上下文信息的问题。
比如下面的测试示例中,故意使得 test_upper 中断言不通过:
import pytestdef test_upper(): assert 'foo'.upper() == 'FOO1'class TestClass: def test_one(self): x = "this" assert "h" in x def test_two(self): x = "hello" with pytest.raises(TypeError): x + []而当使用 pytest 去执行用例时,它会输出详细的(且是多种颜色)上下文信息:
=================================== test session starts ===================================platform darwin -- Python 3.7.1, pytest-4.0.1, py-1.7.0, pluggy-0.8.0rootdir: /Users/prodesire/projects/tests, inifile:plugins: cov-2.6.0collected 3 itemstest.py F.. [100%]======================================== FAILURES =========================================_______________________________________ test_upper ________________________________________ def test_upper():> assert 'foo'.upper() == 'FOO1'E AssertionError: assert 'FOO' == 'FOO1'E - FOOE + FOO1E ? +test.py:4: AssertionError=========================== 1 failed, 2 passed in 0.08 seconds ============================不难看到,pytest 既输出了测试代码上下文,也输出了被测变量值的信息。相比于 nose 和 unittest,pytest 允许用户使用更简单的方式编写测试用例,又能得到一个更丰富和友好的测试结果。
三、用例发现和执行
unittest 和 nose 所支持的用例发现和执行能力,pytest 均支持。 pytest 支持用例自动(递归)发现:
- 默认发现当前目录下所有符合 test_*.py 或 *_test.py 的测试用例文件中,以 test 开头的测试函数或以 Test 开头的测试类中的以 test 开头的测试方法
- 使用 pytest 命令
- 同 nose2 的理念一样,通过在配置文件中指定特定参数,可配置用例文件、类和函数的名称模式(模糊匹配)
pytest 也支持执行指定用例:
- 指定测试文件路径pytest /path/to/test/file.py
- 指定测试类pytest /path/to/test/file.py:TestCase
- 指定测试方法pytest another.test::TestClass::test_method
- 指定测试函数pytest /path/to/test/file.py:test_function
四、测试夹具(Fixtures)
pytest 的测试夹具和 unittest、nose、nose2的风格迥异,它不但能实现 setUp 和 tearDown这种测试前置和清理逻辑,还其他非常多强大的功能。
4.1 声明和使用
pytest 中的测试夹具更像是测试资源,你只需定义一个夹具,然后就可以在用例中直接使用它。得益于 pytest 的依赖注入机制,你无需通过from xx import xx的形式显示导入,只需要在测试函数的参数中指定同名参数即可,比如:
import pytest@pytest.fixturedef smtp_connection(): import smtplib return smtplib.SMTP("smtp.gmail.com", 587, timeout=5)def test_ehlo(smtp_connection): response, msg = smtp_connection.ehlo() assert response == 250上述示例中定义了一个测试夹具 smtp_connection,在测试函数 test_ehlo 签名中定义了同名参数,则 pytest 框架会自动注入该变量。
4.2 共享
在 pytest 中,同一个测试夹具可被多个测试文件中的多个测试用例共享。只需在包(Package)中定义 conftest.py 文件,并把测试夹具的定义写在该文件中,则该包内所有模块(Module)的所有测试用例均可使用 conftest.py 中所定义的测试夹具。
比如,如果在如下文件结构的 test_1/conftest.py 定义了测试夹具,那么 test_a.py 和 test_b.py 可以使用该测试夹具;而 test_c.py 则无法使用。
`-- test_1| |-- conftest.py| `-- test_a.py| `-- test_b.py`-- test_2 `-- test_c.py4.3 生效级别
unittest 和 nose 均支持测试前置和清理的生效级别:测试方法、测试类和测试模块。
pytest 的测试夹具同样支持各类生效级别,且更加丰富。通过在pytest.fixture 中指定 scope 参数来设置:
- function —— 函数级,即调用每个测试函数前,均会重新生成 fixture
- class —— 类级,调用每个测试类前,均会重新生成 fixture
- module —— 模块级,载入每个测试模块前,均会重新生成 fixture
- package —— 包级,载入每个包前,均会重新生成 fixture
- session —— 会话级,运行所有用例前,只生成一次 fixture
当我们指定生效级别为模块级时,示例如下:
import pytestimport smtplib@pytest.fixture(scope="module")def smtp_connection(): return smtplib.SMTP("smtp.gmail.com", 587, timeout=5)4.4 测试前置和清理
pytest 的测试夹具也能够实现测试前置和清理,通过 yield 语句来拆分这两个逻辑,写法变得很简单,如:
import smtplibimport pytest@pytest.fixture(scope="module")def smtp_connection(): smtp_connection = smtplib.SMTP("smtp.gmail.com", 587, timeout=5) yield smtp_connection # provide the fixture value print("teardown smtp") smtp_connection.close()在上述示例中,yield smtp_connection 及前面的语句相当于测试前置,通过 yield 返回准备好的测试资源 smtp_connection; 而后面的语句则会在用例执行结束(确切的说是测试夹具的生效级别的声明周期结束时)后执行,相当于测试清理。
如果生成测试资源(如示例中的 smtp_connection)的过程支持 with 语句,那么还可以写成更加简单的形式:
@pytest.fixture(scope="module")def smtp_connection(): with smtplib.SMTP("smtp.gmail.com", 587, timeout=5) as smtp_connection: yield smtp_connection # provide the fixture valuepytest 的测试夹具除了文中介绍到的这些功能,还有诸如参数化夹具、工厂夹具、在夹具中使用夹具等更多高阶玩法。
五、跳过测试和预计失败
pytest 除了支持 unittest 和 nosetest 的跳过测试和预计失败的方式外,还在 pytest.mark 中提供对应方法:
- 通过 skip装饰器或 pytest.skip函数直接跳过测试
- 通过 skipif按条件跳过测试
- 通过 xfail预计测试失败
示例如下:
@pytest.mark.skip(reason="no way of currently testing this")def test_mark_skip(): ...def test_skip(): if not valid_config(): pytest.skip("unsupported configuration")@pytest.mark.skipif(sys.version_info < (3, 6), reason="requires python3.6 or higher")def test_mark_skip_if(): ...@pytest.mark.xfaildef test_mark_xfail(): ...六、子测试/参数化测试
pytest 除了支持 unittest 中的 TestCase.subTest,还支持一种更为灵活的子测试编写方式,也就是 参数化测试,通过 pytest.mark.parametrize 装饰器实现。
在下面的示例中,定义一个 test_eval 测试函数,通过 pytest.mark.parametrize 装饰器指定 3 组参数,则将生成 3 个子测试:
@pytest.mark.parametrize("test_input,expected", [("3+5", 8), ("2+4", 6), ("6*9", 42)])def test_eval(test_input, expected): assert eval(test_input) == expected示例中故意让最后一组参数导致失败,运行用例可以看到丰富的测试结果输出:
========================================= test session starts =========================================platform darwin -- Python 3.7.1, pytest-4.0.1, py-1.7.0, pluggy-0.8.0rootdir: /Users/prodesire/projects/tests, inifile:plugins: cov-2.6.0collected 3 itemstest.py ..F [100%]============================================== FAILURES ===============================================__________________________________________ test_eval[6*9-42] __________________________________________test_input = '6*9', expected = 42 @pytest.mark.parametrize("test_input,expected", [("3+5", 8), ("2+4", 6), ("6*9", 42)]) def test_eval(test_input, expected):> assert eval(test_input) == expectedE AssertionError: assert 54 == 42E + where 54 = eval('6*9')test.py:6: AssertionError================================= 1 failed, 2 passed in 0.09 seconds ==================================若将参数换成 pytest.param,我们还可以有更高阶的玩法,比如知道最后一组参数是失败的,所以将它标记为 xfail:
@pytest.mark.parametrize( "test_input,expected", [("3+5", 8), ("2+4", 6), pytest.param("6*9", 42, marks=pytest.mark.xfail)],)def test_eval(test_input, expected): assert eval(test_input) == expected如果测试函数的多个参数的值希望互相排列组合,我们可以这么写:
@pytest.mark.parametrize("x", [0, 1])@pytest.mark.parametrize("y", [2, 3])def test_foo(x, y): pass上述示例中会分别把 x=0/y=2、x=1/y=2、x=0/y=3和x=1/y=3带入测试函数,视作四个测试用例来执行。
七、测试结果输出
pytest 的测试结果输出相比于 unittest 和 nose 来说更为丰富,其优势在于:
- 高亮输出,通过或不通过会用不同的颜色进行区分
- 更丰富的上下文信息,自动输出代码上下文和变量信息
- 测试进度展示
- 测试结果输出布局更加友好易读
八、插件体系
pytest 的插件十分丰富,而且即插即用,作为使用者不需要编写额外代码。
此外,得益于 pytest 良好的架构设计和钩子机制,其插件编写也变得容易上手。
九、总结
三篇关于 Python 测试框架的介绍到这里就要收尾了。写了这么多,各位看官怕也是看得累了。我们不妨罗列一个横向对比表,来总结下这些单元测试框架的异同:
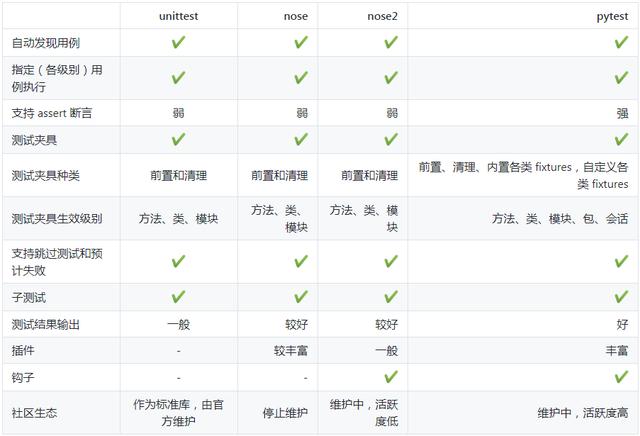
Python 的单元测试框架看似种类繁多,实则是一代代的进化,有迹可循。抓住其特点,结合使用场景,就能容易的做出选择。
若你不想安装或不允许第三方库,那么 unittest 是最好也是唯一的选择。反之,pytest 无疑是最佳选择,众多 Python 开源项目都是使用 pytest 作为单元测试框架。
以上内容就是本篇的全部内容以上内容希望对你有帮助。
如果对接口、性能、自动化测试、面试经验交流等感兴趣的,可以关注我的头条号,我会不定期的发放免费的资料,这些资料都是从各个技术网站搜集、整理出来的,如果你有好的学习资料可以私聊发我,我会注明出处之后分享给大家。欢迎分享,欢迎评论,欢迎转发。需要资料的同学可以关注小编+转发文章+私信【测试资料】
