金融行业网站开发百度网站的优点
什么是VLAN
VLAN(Virtual LAN),翻译成中文是“虚拟局域网”。可以看做是在一个物理局域网络上搭建出几个逻辑上分离的几个局域网。举个例子来说,如果一个交换机划分为两个VLAN,则相当于这台交换机逻辑上划分为两个交换机。
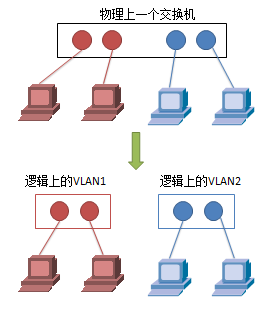
VLAN的一个简单直观说明:物理上一个交换机,分为逻辑上两个分离的交换机
上面这个简单例子是对一台交换机上的VLAN划分,实际上VLAN也可以跨越多台交换机,本质上VLAN是一个网络层次上的概念,将整个网络划分为多个逻辑上隔离的网络(一个VLAN就是一个独立的广播域)比如下图的VLAN2和VLAN5。
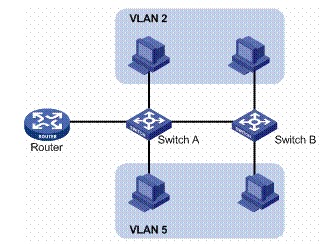
跨越多台交换机的VLAN
那么我们为什么要引入VLAN的概念,VLAN究竟有哪些好处,总结起来主要有下面几点:
更安全:数据包仅在本VLAN内传递。
由于配置了VLAN后,一个VLAN的数据包不会发送到另一个VLAN,这样,其他VLAN的用户的网络上是收不到任何该VLAN的数据包,这样就确保了该VLAN的信息不会被其他VLAN的人窃听,从而实现了信息的保密。
更高效:泛洪转发仅在本VLAN内复制。
按照802.1D透明网桥的算法,如果一个数据包找不到MAC表,那么交换机就会将该数据包向除接收端口以外的其他所有端口发送,这就是桥的泛洪转发。(典型的广播方式包括组播报文,广播报文,以及未知单播报文都会进行泛洪转发)。这样的结果,毫无疑问极大的浪费了带宽,如果配置了VLAN,那么,当一个数据包需要泛洪转发时,交换机只会将此数据包发送到所有属于该VLAN的其他端口,而不是所有的交换机的端口,这样,就将数据包限制到了一个VLAN内。在一定程度上可以节省带宽。
更方便:不改变物理组网的情况下,灵活进行逻辑网络的变更。
使用VLAN的最终目标就是建立虚拟工作组模型,例如,在企业网中,同一个部门的就好象在同一个LAN上一样,很容易的互相访问,交流信息,同时,所有的广播包也都限制在该虚拟LAN上,而不影响其他VLAN的人。一个人如果从一个办公地点换到另外一个地点,而他仍然在该部门,那么,该用户的配置无须改变;同时,如果一个人虽然办公地点没有变,但他更换了部门,那么,只需网络管理员更改一下该用户的配置即可。这个功能的目标就是建立一个动态的组织环境,当然,这只是一个理想的目标,要实现它,还需要一些其他方面的支持。
如何实现VLAN功能
1. 如何识别VLAN报文
要使网络设备能够分辨不同VLAN的报文,需要在报文中添加标识VLAN的字段。由于普通交换机工作在OSI模型的数据链路层,只能对报文的数据链路层封装进行识别。因此,如果添加识别字段,也需要添加到数据链路层封装中。
IEEE于1999年颁布了用以标准化VLAN实现方案的IEEE 802.1Q协议标准草案,对带有VLAN标识的报文结构进行了统一规定。
无VLAN的传统的以太网数据帧格式:目的MAC地址和源MAC地址之后封装的是上层协议的类型字段,
DA表示目的MAC地址
SA表示源MAC地址
Type表示报文所属协议类型。

传统无VLAN的二层报文
增加VLAN Tag支持的以太网帧格式:IEEE 802.1Q协议规定在目的MAC地址和源MAC地址之后封装4个字节的VLAN Tag,用以标识VLAN的相关信息。VLAN Tag包含四个字段,分别是TPID(Tag Protocol Identifier,标签协议标识符)、Priority、CFI(Canonical Format Indicator,标准格式指示位)和VLAN ID。
TPID用来判断本数据帧是否带有VLAN Tag,长度为16bit,缺省取值为0x8100。
Priority表示报文的802.1P优先级,长度为3bit,相关内容请参见“QoS分册”中的“QoS配置”。
CFI字段标识MAC地址在不同的传输介质中是否以标准格式进行封装,长度为1bit,取值为0表示MAC地址以标准格式进行封装,为1表示以非标准格式封装,缺省取值为0。
VLAN ID标识该报文所属VLAN的编号,长度为12bit,取值范围为0~4095。由于0和4095为协议保留取值,所以VLAN ID的取值范围为1~4094。
网络设备利用VLAN ID来识别报文所属的VLAN,根据报文是否携带VLAN Tag以及携带的VLAN Tag值,来对报文进行处理。

支持VLAN字段以后的二层报文
2. 交换机如何转发VLAN报文
要说明交换机如何转发报文,先得说明一下交换机支持VLAN时用到的几个专用术语:
端口类型:VLAN交换机的端口一般可以分为几大类:
Access端口:一般用于交换机与终端之间,该类端口仅归属于一个VLAN。Access链路上的报文没有VLAN tag,与传统报文保持兼容。但交换机的Access端口上回配置Vlan。这样所有从该Access链路上收到的报文都归属于Access端口所归属的Vlan。(核心概念:报文兼容,没有vlan-tag)
Trunk端口:一般交换机与交换机之间,该类型端口允许多个VLAN的报文通过。该端口所在的链路上的报文需要有VLAN tag。(核心概念:除默认Vlan外,其他VLAN报文有vlan-tag)
Hybrid端口:Hybrid类型的端口可以允许多个VLAN通过,可以接收和发送多个VLAN的报文,可以用于交换机之间连接,也可以用于连接用户的计算机。Hybrid端口和Trunk端口在接收数据时,处理方法是一样的,唯一不同之处在于发送数据时:Hybrid端口可以允许多个VLAN的报文发送时不打标签,而Trunk端口只允许缺省VLAN的报文发送时不打标签。(核心概念:哪些vlan打tag,哪些不打tag可以手工配置)
术语:默认VLAN-ID(或者缺省VLAN-ID,PvidVlan,Native Vlan,都是一个意思):简而言之,收报文:如果是没有tag,则认为来自于默认vlan;发报文:如果是该vlan的报文则不打VLAN tag
Access端口只属于1个VLAN,所以它的缺省VLAN就是它所在的VLAN,不用设置;
Hybrid端口和Trunk端口属于多个VLAN,所以需要设置缺省VLAN ID。缺省情况下,Hybrid端口和Trunk端口的缺省VLAN为VLAN 1 。如果设置了端口的缺省VLAN ID,当端口接收到不带VLAN Tag的报文后,则认为报文的VLAN ID是缺省VLAN-ID;当端口发送报文时,如果该报文的VLAN ID与端口缺省的VLAN ID相同,则系统将去掉报文的VLAN Tag,然后再发送该报文。
下面具体介绍着几种端口的工作原理
2.1 Access端口
这一类端口只有一个唯一的VLAN。通常由于交换机与终端的连接。为了保持与已有终端的兼容性,在设计VLAN相关协议时有这样一个约束:端口发送和接收的报文格式都不允许修改,也就是说,这一类接口上收发的报文都不带VLAN信息。(Untagged)。
既然报文中不带VLAN信息,又要满足VLAN隔离性需求,则必然在端口上要进行VLAN-ID的设置(这个VLAN称为端口的PVID)。
2.2 Access端口的报文转发流程
Acess端口收报文:
收到个报文判断是否有VLAN信息:
如果没有则打上端口 PVID并进行交换、转发,
如果有则直接丢弃(缺省)
Acess端口发报文:
Access端口发送非常简单,将报文VLAN信息剥离,直接发送出去
2.2 Access端口如何划分VLAN
为了方便用户使用,各设备厂商实现了多种方式来进行VLAN划分,总的来说,有静态方式和动态方式两大类:
静态方式:通过用户手工配置方式,来指定某个端口属于哪个VLAN,静态方式也成为基于端口的VLAN。当网络中的计算机数目超过一定数字(比如数百台)后,这些配置操作就会变得烦杂无比。并且,客户机每次变更所连端口,都必须同时更改该端口所属VLAN的设定——这显然不适合那些需要频繁改变拓补结构的网络。
动态方式:动态VLAN则是根据每个端口所连的计算机,随时改变端口所属的VLAN。这可以减轻配置人员的负担。动态VLAN又可以进一步分为下面3类:
基于MAC地址的VLAN(MAC Based VLAN)
基于MAC地址的VLAN,就是通过查询并记录端口所连计算机上网卡的MAC地址来决定端口的所属。假定有一个MAC地址“A”被交换机设定为属于VLAN “10”,那么不论MAC地址为“A”的这台计算机连在交换机哪个端口,该端口都会被划分到VLAN 10中去。
基于子网的VLAN(Subnet Based VLAN)
基于子网的VLAN,则是通过所连计算机的IP地址,来决定端口所属VLAN的。不像基于MAC地址的VLAN,即使计算机因为交换了网卡或是其他原因导致MAC地址改变,只要它的IP地址不变,就仍可以加入原先设定的VLAN。
基于协议或用户的VLAN(User Based VLAN)
基于协议或用户的VLAN,则是根据交换机各端口所连的计算机发送报文的协议,或者计算机上当前登录的用户,来决定该端口属于哪个VLAN。这里的用户识别信息,一般是计算机操作系统登录的用户,比如可以是Windows域中使用的用户名。这些用户名信息,属于OSI第四层以上的信息。
2.4 Trunk端口
其实原则上,有了Access口,就可以完成VLAN所需要的完整功能了。比如:交换机上也使用Access口进行连接,每一个端口一个VLAN进行隔离。比如下面的例子,两个VLAN,全部使用Access接口来构建。
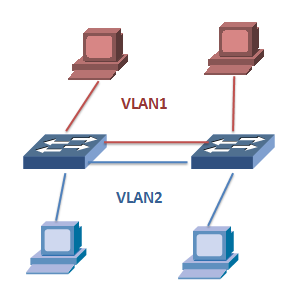
全部使用ACCESS接口构建VLAN网络
但这儿存在一个问题,因为一个Access口仅属于一个VLAN,如果两个交换机配置了成百上千个VLAN,这些VLAN需要跨交换机组网时,意味着两个交换机之间需要连接成百上千根的Access口链路。这样组网成本太高了。
为了解决这一问题,提出了Trunk端口的概念,Trunk端口允许接受和发送多个VLAN的报文,这些报文都打上VLAN-tag,用来标示每一个报文属于哪个VLAN。这样,交换机之间就只需要一个Trunk链路,就可以将多个VLAN连接起来。
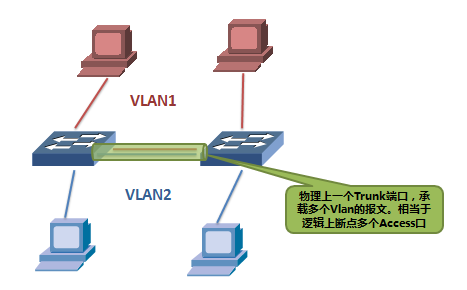
Trunk端口,用于连接交换机,充当逻辑上的多个链路
2.5 Trunk端口的报文收发流程
Trunk端口收报文:
Trunk端口收到一个报文,判断是否有VLAN信息:
如果报文中没有VLAN-tag,则打上端口的PVID,并进行交换转发,
如果报文中有Vlan-tag,进一步判断trunk端口是否允许该 VLAN的数据进入:
如果可以则转发
否则丢弃
Trunk端口发报文:
比较端口的PVID和将要发送报文的VLAN信息:
如果两者相等则剥离VLAN信息,再发送
如果不相等则直接发送
2.6 Hybrid端口
Hybrid端口和Trunk端口的相同之处在于两种链路类型的端口都可以允许多个VLAN的报文发送时打标签;不同之处在于Hybrid端口可以允许多个VLAN的报文发送时不打标签,而Trunk端口只允许缺省VLAN的报文发送时不打标签。
对于Hybrid端口来说,可以同时属于多个VLAN。这些VLAN分别是该Hybrid端口的PVID,以及手工配置的”untagged”及”tagged”方式的VLAN。
2.7 Hybrid端口的报文收发流程
Hybrid端口收报文: 与Trunk端口手报文流程完全相同。
Hybrid端口收到一个报文,判断是否有VLAN信息:
如果报文中没有VLAN-tag,则打上端口的PVID,并进行交换转发,
如果报文中有Vlan-tag,进一步判断trunk端口是否允许该 VLAN的数据进入:
如果可以则转发
否则丢弃
Hybrid端口发报文:
判断该VLAN在本端口属性(哪些vlan需要打tag,哪些不需要打tag,是手工配置的):
如果需要tag,则tag后直接发送(同Trunk端口)
如果不需要tag,则剥离tag后发送(同Access端口)因为Hybrid端口的行为是access和trunk的混合模式,所以称为Hybrid
2.8 Hybrid的应用场景:
通常,可以使用Hybrid对相同网段的主机进行访问权限的控制。比如,通过配置Hybrid端口,可以让改端口的主机同时归属于多个VLAN,并与多个VLAN的主机进行通讯。
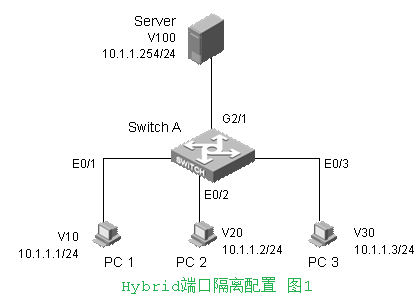
应用场景1:PC间隔离
组网需求:
PC1和PC2之间可以互访;
PC1和PC3之间可以互访;
PC1、PC2和PC3都可以访问服务器;
配置说明:
E0/1: Hybrid端口,归属V10, 同时untag加入V20,V30,V100(PC1访问PC2,PC3,Server)
E0/2: Hybrid端口,归属V20, 同时untag加入V10,V100(PC2访问PC1,Server)
E0/3: Hybrid端口,归属V30, 同时untag加入V10,V100(PC3访问PC1,Server)
G2/1: Hybrid端口,归属V100, 同时untag加入V10,V20,V30(服务器访问PC1,PC2,PC3)
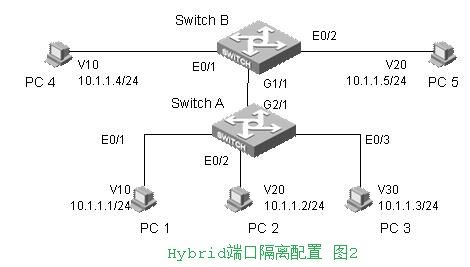
应用场景2
组网需求
PC1和PC3之间可以互访;
PC2和PC3之间可以互访;
PC1和PC4之间可以互访;
PC2和PC5之间可以互访;
其余PC之间均禁止互相访问。
配置说明:
SwitchA:
E0/1: Hybrid端口,加入V10,同时untag加入V30
E0/2: Hybrid端口,加入V20,同时untag加入V30
E0/3: Hybrid端口,加入V30,同时untag加入V10,V20.
G2/1: Hybrid端口,(不加入某个VLAN),tagged加入V10,V20。
SwitchB:
E0/1: Access端口,加入V10
E0/2: Access端口,加入V20
E0/1: Hybrid端口,(不加入某个VLAN),tagged加入V10,V20。
注:交换机间的Hybrid端口,等价于Trunk端口
注意事项
配置Trunk端口或Hybrid端口,并利用Trunk端口或Hybrid端口发送多个VLAN报文时一定要注意:本端端口和对端端口的缺省VLAN ID(端口的PVID)要保持一致。
