北京网站建设公司那个好西安网站建设公司
本文的内容是mysql8的下载与安装。主要讲的是两点:从官方网站下载MySQL8安装和从集成环境安装MySQL8。

一、从官方网站下载MySQL8.0安装
MySQL8.0官方下载地址是:(见图)
官方正式版的最新版本是8.0.34,也推出了创新版8.1.0,也有正在使用的5.7.43版本,我们选择稳定的8.0.34即可,平台选windows,如图:
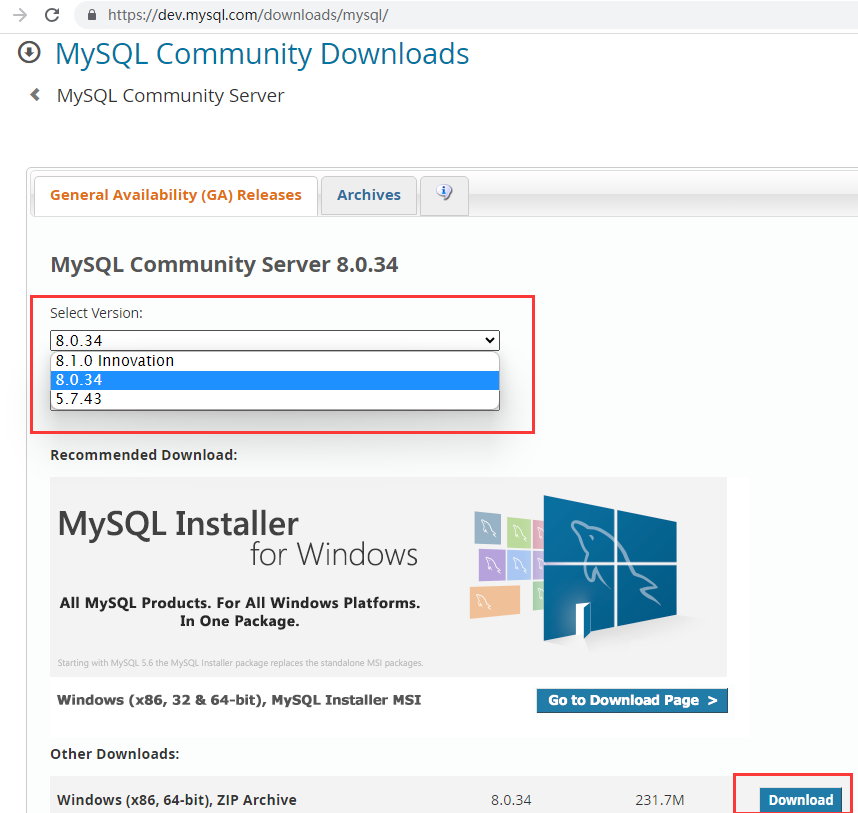
本站教程,早就从集成环境安装了,就不在进行一步一步的演示了,有下载地址了,下载和安装,我相信没有人不会的了。
二、从集成环境安装MySQL8。
正常情况下,直接下载,安装即可,本站的教程不是直接在官方网站下载安装的,而是通过php开发环境套件安装的,MySQL8.0的安装在《搭建PHP8集成环境》一文中安装了,没有阅读的点击此文阅读。如图:
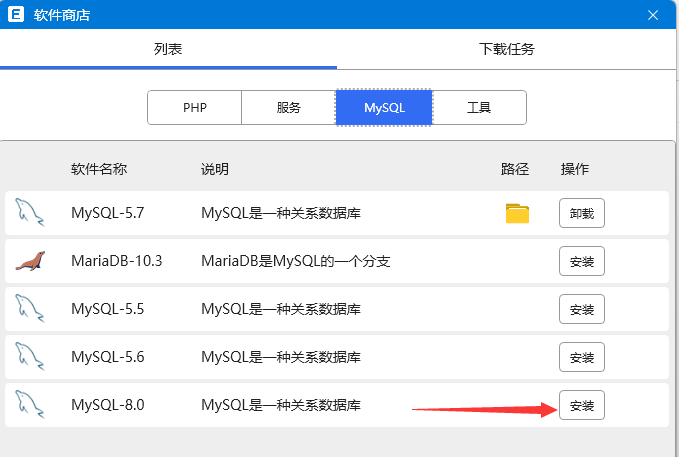
接下来的数据操作,也是从这个套件入口进行操作,为了方便读者学习,建议和我一样安装PHP8的集成环境套件phpenv来安装MySQL8。
当然不管是从官方下载安装的还是从集成环境phpenv里面安装MySQL8,的所实现的功能都是一样的,不过如果是安装官方下载版的,会集成安装了很多配套的软件,如:MySQL Server、MySQL Workbench、MySQL Shell、MySQL Router等。
拿MySQL Workbench图形化管理工具来说,这个可以直接创建数据库和数据表。我们使用集成环境安装的MySQL8也集成了其他图形化工具,用于新建数据库和数据表,所以完全不用担心相关的问题。
到此为止,从官方网站下载MySQL8安装和从集成环境安装MySQL8就讲解完毕,教程很简单,大家记得实操即可。
