北京高端网站定制公司哪家好公司名称logo图片
收集了各大公司的面试经验,现整理出来,希望能给正在找工作的志同道合的小伙伴一些指引,本文会持续更新的哦。
1、 CPU 和 GPU的区别
一个是通用计算,一个是专用计算。
CPU主要负责操作系统和应用程序,GPU主要负责跟显示相关的数据处理,GPU的活CPU一般都可以干,但是效率低下。CPU和GPU之所以大不相同,是由于其设计目标的不同,它们分别针对了两种不同的应用场景。CPU需要很强的通用性来处理各种不同的数据类型,同时又要逻辑判断又会引入大量的分支跳转和中断的处理。这些都使得CPU的内部结构异常复杂。而GPU面对的则是类型高度统一的、相互无依赖的大规模数据和不需要被打断的纯净的计算环境。
2、 推荐的算法有哪些
推荐应该说分为两类:个性化推荐和非个性化推荐,“让全局优秀的内容被大家看到”应该算是非个性化推荐,热门榜单/最多观看这类方法可以简单解决这个问题;不同的人对于“好”的理解不一样,换句话说也就是偏好不同,所以推荐新加入的好内容我认为是个性化推荐问题。
个性化推荐的两个主要思想八个字概括之:物以类聚、人以群分。主要的方法及变种应该有很多,像协同过滤、基于内容的推荐、基于标签的推荐等等。
3、 协同过滤是怎么实现的
4、 熟悉的Linux命令,查看磁盘空间的命令,如何找到一个文件中含有aaa 和 bbb和行
查看磁盘空间命令:df –lh
grep -rn "aaa"&& "bbb" *
* : 表示当前目录所有文件,也可以是某个文件名
-r 是递归查找
-n 是显示行号
-R 查找所有文件包含子目录
-i 忽略大小写
5、白盒和黑盒测试的方法有哪些
白盒测试:语句覆盖、条件覆盖、判定覆盖、判定条件覆盖、条件组合覆盖
黑盒测试:等价划分法、边界值法、因果图法、猜错法、随机数法
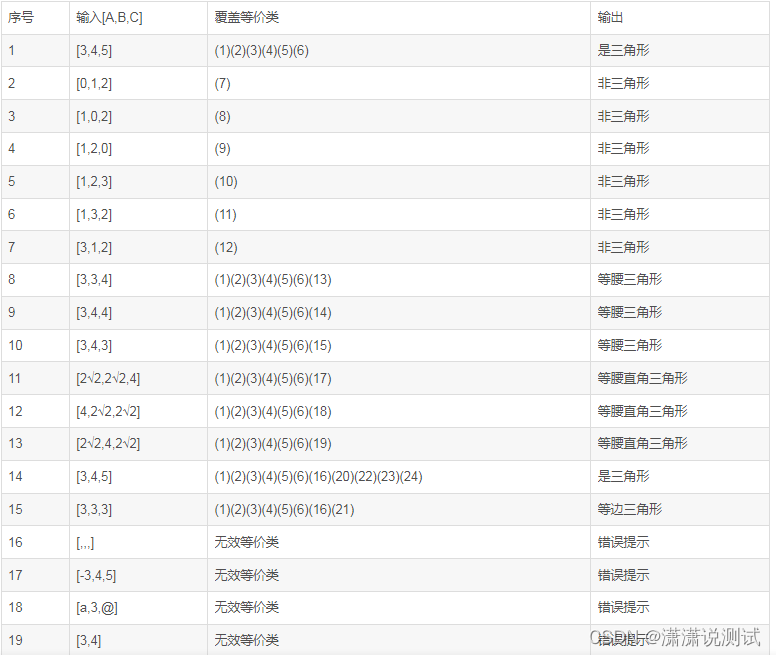
6、如何测试一个三角形是否是一个等腰三角形,写出测试用例
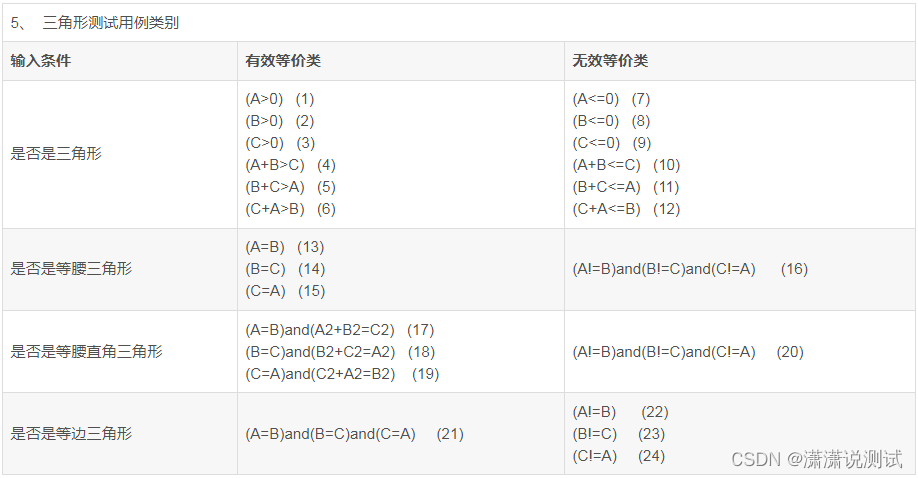
三角形测试用例:用最少的测试用例覆盖所有的有效等价类,而无效等价类每个类型都要覆盖到
7、排序的算法以及时间复杂度

8、对一个自动贩卖机进行功能测试
按照功能测试的划分等价类来测试
有效的等价类有:
金额刚够,顺利出货
金额超出,找零出货
金额超出, 没钱找零,出货.
金额不足,进行提示,把货币退出
金额足够,取消交易
假币,不出
无效等价类:
投入金额,不出货,不找零
投入金额,不出货,退钱
金额超出,出货,不找零
金额超出,不出货,找零
金额不足,出货,找零l
金额不足,出货,不找零
金额不足,不出货,不退款
金额刚够,不出货,退款
金额刚够,出货,找零
金额刚够,不出货,找零
不投金额,直接出货
9、为什么选择软件测试这个岗位
现在的软件行业日新月异,发展的如日中天,同行之间的竞争更是此起彼伏,稍有不慎就会面临破产,其中产品的质量更是重中之重,出现一点点小问题就会导致用户量骤减,由于我国的互联网行业起步较晚,在质量把控这方面没有国外做到到位,但我相信,软件测试行业将会有很大的发展前景,我也能在这个领域一展我的抱负。
10、应聘软件测试的优势与劣势
优势:
1、 我有足够的责任心
2、 有很好的学习能力
3、 适应新事物新环境很迅速
4、 有计算机相关理论基础
劣势:
1、 缺少社会经验
2、 编程能力较弱
11、有50个红球,50个蓝球,如何放入两个盒子中使得拿到红球的概率最大
不管你怎么放,概率都是二分之一。
譬如,红的全放一个箱子,那么只要你从俩个箱子中选择这个箱子,就一定是红球,为二分之一。
二,如果一个箱子放一半红球一半篮球,那么你随便抽一个箱子,都是二分之一的概率抽到红球。
三,任意情况,如,箱子一有30个红球,那么红球的概率,为1/2*30/50+1/2*20/50,还是二分之一
12、有5个强盗分100枚金币,从1号开始进行分配,必须有半数服从分配才通过,否则否则1被毙掉,由2号开始分,问1号要怎样分才能使自己利益最大化
采用反推过来的算法:
5号表决时,形成的状态是:
1得到0个宝石,死
2得到0个宝石,死
3得到0个宝石,死
4得到0个宝石,死
5得到100个宝石,活,同意
原因:
不用讲了,能轮到5号表决当然他独吞了
但是也会与题目违背了,因为前面几个海盗都是傻瓜差不多
4号表决时,形成的状态是:
1得到0个宝石,死
2得到0个宝石,死
3得到0个宝石,死
4得到100个宝石,活,同意
5得到0个宝石,活,不同意
原因:
这时只剩下二比一的情况,只要自己同意即可达到半数而通过表决,不存在生命危险
但是3号也不是白痴
3号表决时,形成的状态是:
1得到0个宝石,死
2得到0个宝石,死
3得到99个宝石,活,同意
4得到0个宝石,活,不同意
5得到1个宝石,活,同意
轮到3号时,他只要给5号1个宝石就够了
原因:
因为5号会意识到,一旦轮到4号时他就一个也得不到,现在能得到1个宝石已经是给了面子了
但2号也很聪明的,能否轮到他只是一种期待,来看看2号的情况
2号表决时,形成的状态是:
1得到0个宝石,死
2得到99个宝石,活,同意
3得到0个宝石,活,不同意
4得到1个宝石,活,同意
5得到0个宝石,活,不同意
要是轮到此海盗他必会拿走99颗宝石,然后给4号1颗即可!
为什么? 原因是:
4号已经意识到,要是轮到3号表决时,他将一个也得不到,所以这时有点收获,固然同意了
这时也考虑到:
3号不可巴结,会损失太多,因为如果只是单单给3号的话,他随时都可以不同意而获得表决权
5号也可巴结,但需要2颗宝石,不合算,因为5号也知道即使下一轮也是拿定一颗宝石的
1号:此海盗当然也聪明了
从上述看出,既然轮到2号的局势已定,那他早已知道后面的海盗心里想什么了
也就是简单的说,他们清楚认识到,轮到2号时,3号和5号得不到宝石!
那么这样的话,事情就好办多了,给他们一人一颗自然就搞定了!
所以,1海海盗毅然作出决定,分别给3号和5号各1颗宝石
最终结局的状态是:
1得到98个宝石,活,同意
2得到 0个宝石,活,不同意
3得到 1个宝石,活,同意
4得到 0个宝石,活,不同意
5得到 1个宝石,活,同意
即:98,0,1,0,1 (达到1号利益最大化)
13、如果没网,可能是什么原因造成的
一、使用的是有线网线
1、路由器数据堵塞,一般重启路由可以解决;如果重启仍不能解决,可能是运营商的问题了,及时电话咨询;
2、自身电脑问题,连接有线网的情况,这种情况很少见;
二、连接的是无线网
1、路由器问题,重启路由试试;也不排除线路问题;
2、无线接收器问题,看灯闪烁是否正常,可以尝试拔队,重新插上;
3、也可以尝试把无线禁用,然后重新开无线网络;
4、重新安装无线网驱动试试;
14、怎样测一张A4纸
1.纸张的质地,是否为纸张
2.纸张的品质,是草木、皮革。。。
3.纸张的类别,是否为白纸
4.纸张的功能,能否书写,图画等
5.纸张的兼容性,水笔、油笔、铅笔是都都能正常书写
6.纸张的扩展性,折叠、拉伸
7.纸张的安全性,纸张的生产工艺是否安全,纸张有无有毒性物质
8.纸张的结构
9.纸张的性能:对各种笔的吸油性是否够快
15、数据库知识:姓名,班级、课程名、分数
1、求语文分数最高的学生
Select 姓名,max(分数)from 表名where 课程名=“语文”
2.求每个班语文成绩最高的学生
16、三次握手,每次发送的内容都是什么
第一次握手:建立连接时,客户端发送syn包(syn=j)到服务器,并进入SYN_SENT状态,等待服务器确认;SYN:同步序列编号(Synchronize Sequence Numbers)。
第二次握手:服务器收到syn包,必须确认客户的SYN(ack=j+1),同时自己也发送一个SYN包(syn=k),即SYN+ACK包,此时服务器进入SYN_RECV状态;
第三次握手:客户端收到服务器的SYN+ACK包,向服务器发送确认包ACK(ack=k+1),此包发送完毕,客户端和服务器进入ESTABLISHED(TCP连接成功)状态,完成三次握手。
补充:
完成三次握手,客户端与服务器开始传送数据,在上述过程中,还有一些重要的概念:
未连接队列
在三次握手协议中,服务器维护一个未连接队列,该队列为每个客户端的SYN包(syn=j)开设一个条目,该条目表明服务器已收到SYN包,并向客户发出确认,正在等待客户的确认包。这些条目所标识的连接在服务器处于SYN_RECV状态,当服务器收到客户的确认包时,删除该条目,服务器进入ESTABLISHED状态。
17、关闭TCP连接:改进的三次握手
对于一个已经建立的连接,TCP使用改进的三次握手来释放连接(使用一个带有FIN附加标记的报文段)。TCP关闭连接的步骤如下:
第一步,当主机A的应用程序通知TCP数据已经发送完毕时,TCP向主机B发送一个带有FIN附加标记的报文段(FIN表示英文finish)。
第二步,主机B收到这个FIN报文段之后,并不立即用FIN报文段回复主机A,而是先向主机A发送一个确认序号ACK,同时通知自己相应的应用程序:对方要求关闭连接(先发送ACK的目的是为了防止在这段时间内,对方重传FIN报文段)。
第三步,主机B的应用程序告诉TCP:我要彻底的关闭连接,TCP向主机A送一个FIN报文段。
第四步,主机A收到这个FIN报文段后,向主机B发送一个ACK表示连接彻底释放。
18、为什么要采用三次握手,两次不行吗?
保活计时器:
为了防止已失效的连接请求报文段突然又传送到了服务端,因而产生错误。
设想有这样的情况:客户端已主动与服务器建立了TCP连接,但后来客户端的主机突然出现故障。
通常设为2小时。若2小时没有收到客户端的数据,服务器就发送一个探测报文段,以后则每隔75分钟发送一次。若一连发送10个探测报文段后仍无客户端的响应,服务器就认为客户端出现了故障,接着就关闭这个连接。
19、为什么连接的时候是三次握手,关闭的时候却是四次握手?
答:因为当Server端收到Client端的SYN连接请求报文后,可以直接发送SYN+ACK报文。其中ACK报文是用来应答的,SYN报文是用来同步的。但是关闭连接时,当Server端收到FIN报文时,很可能并不会立即关闭SOCKET,所以只能先回复一个ACK报文,告诉Client端,"你发的FIN报文我收到了"。只有等到我Server端所有的报文都发送完了,我才能发送FIN报文,因此不能一起发送。故需要四步握手。
20、为什么TIME_WAIT状态需要经过2MSL(最大报文段生存时间)才能返回到CLOSE状态?
答:虽然按道理,四个报文都发送完毕,我们可以直接进入CLOSE状态了,但是我们必须假象网络是不可靠的,有可以最后一个ACK丢失。所以TIME_WAIT状态就是用来重发可能丢失的ACK报文。
21、微信发送消息功能的测试
1、功能测试
图片、文字(大段文字)、小视频、语音)是否发送顺利,数据有没有丢失、有没有延迟,一个人发了100遍同样的数据能否发送成功,群发功能
2、性能测试
并发度,响应时间,系统资源占用、压力测试、兼容性测试(硬件兼容和软件兼容)、还有就是考虑多端登录消息的同步
22、main函数执行之前都发生了什么
23、fidler抓包原理
Fiddler是一款非常流行并且实用的http抓包工具,它的原理是在本机开启了一个http的代理服务器,然后它会转发所有的http请求和响应,因此,它比一般的firebug或者是chrome自带的抓包工具要好用的多。不仅如此,它还可以支持请求重放等一些高级功能。显然它是可以支持对手机应用进行http抓包的。
24、设计测试用例有哪些方法
黑盒测试:等价划分法、边界值判定、因果图、错误猜测
白盒测试:语句覆盖、条件覆盖、判定覆盖、条件/判定覆盖、条件组合覆盖
25、Vim怎么删除行
dd 删除一整行
D d$ 删除光标位置到本行结尾
d0 删除光标位置到本行开头
26、Linux怎么查看大文件,怎么实时查看文件
[root@getlnx01 u03]# find . -type f -size +800M -print0 | xargs -0 ls –l
27、性能测试有哪些
负载测试、压力测试、疲劳性测试、容量测试
28、TCP的拥塞控制
29、http中的get和post请求的区别
1、GET请求,请求的数据会附加在URL之后,以?分割URL和传输数据,多个参数用&连接。URL的编码格式采用的是ASCII编码,而不是uniclde,即是说所有的非ASCII字符都要编码之后再传输。
POST请求:POST请求会把请求的数据放置在HTTP请求包的包体中。上面item=bandsaw就是实际的传输数据。因此,GET请求的数据会暴露在地址栏中,而POST请求则不会。
2、传输数据的大小
在HTTP规范中,没有对URL的长度和传输的数据大小进行限制。但是在实际开发过程中,对于GET,特定的浏览器和服务器对URL的长度有限制。因此,在使用GET请求时,传输数据会受到URL长度的限制。
对于POST,由于不是URL传值,理论上是不会受限制的,但是实际上各个服务器会规定对POST提交数据大小进行限制,Apache、IIS都有各自的配置。
3、安全性
POST的安全性比GET的高。这里的安全是指真正的安全,而不同于上面GET提到的安全方法中的安全,上面提到的安全仅仅是不修改服务器的数据。比如,在进行登录操作,通过GET请求,用户名和密码都会暴露再URL上,因为登录页面有可能被浏览器缓存以及其他人查看浏览器的历史记录的原因,此时的用户名和密码就很容易被他人拿到了。除此之外,GET请求提交的数据还可能会造成Cross-site request frogery攻击
30、怎么确认post请求发送完毕
31、专利是第一作者么
不一定
32、loadrunner用来干了什么
做性能测试用的。测试软件的性能、压力、负载情况、服务器的响应时间,吞吐量、监控服务器、数据库的性能指标。等等。总之很强大。
最后感谢每一个认真阅读我文章的人,礼尚往来总是要有的,虽然不是什么很值钱的东西,如果你用得到的话可以直接拿走:

这些资料,对于【软件测试】的朋友来说应该是最全面最完整的备战仓库,这个仓库也陪伴上万个测试工程师们走过最艰难的路程,希望也能帮助到你!

